题目内容
已知点M(x,y)满足
,则
的最大值为 .
|
| 2x+y |
| 2x+6 |
考点:简单线性规划
专题:不等式的解法及应用
分析:将目标函数进行化简,利用两点间的斜率公式,利用数形结合即可得到结论.
解答:
解:设z=
,
则z=
=1+
=1+
•
,
设k=
,
则z=1+
k,
只需求出k的最大值即可,
k=
的几何意义为动点P(x,y)与定点(-3,6)连线的斜率.
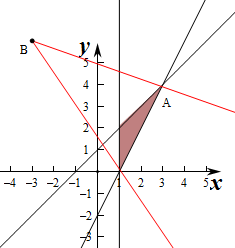
作出不等式组对应的平面区域如图:
由图象可知当点P位于点A时,直线AB的斜率k最大.
由
,解得
,
即A(3,4),此时k=
=
=-
=-
,
∴z=1+
k=1+
×(-
)=1-
=
,
故答案为:
| 2x+y |
| 2x+6 |
则z=
| 2x+6+y-6 |
| 2x+6 |
| y-6 |
| 2x+6 |
| 1 |
| 2 |
| y-6 |
| x+3 |
设k=
| y-6 |
| x+3 |

则z=1+
| 1 |
| 2 |
只需求出k的最大值即可,
k=
| y-6 |
| x+3 |
作出不等式组对应的平面区域如图:
由图象可知当点P位于点A时,直线AB的斜率k最大.
由
|
|
即A(3,4),此时k=
| y-6 |
| x+3 |
| 4-6 |
| 3+3 |
| 2 |
| 6 |
| 1 |
| 3 |
∴z=1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 5 |
| 6 |
故答案为:
| 5 |
| 6 |
点评:本题主要考查线性规划的应用,以及分式的化简,利用两点间的斜率公式是解决本题的关键,本题综合性较强,难度较大.

练习册系列答案
相关题目
 如图,已知P是矩形ABCD内任意一点,延长BP交AD于E,延长DP交AB于F,延长CP交矩形的外接圆于G.求证:GE⊥GF.
如图,已知P是矩形ABCD内任意一点,延长BP交AD于E,延长DP交AB于F,延长CP交矩形的外接圆于G.求证:GE⊥GF.