题目内容
在含有3件次品的5件产品中,任取2件,试求:
(Ⅰ)取到的次品数X的分布列;
(Ⅱ)至多有1件次品的概率.
(Ⅰ)取到的次品数X的分布列;
(Ⅱ)至多有1件次品的概率.
考点:离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)由题意知X=0,1,2,分别求出相应的概率,由此能求出取到的次品数X的分布列.
(Ⅱ)至多有1件次品的概率p=P(X=0)+P(X=1),由此能求出结果.
(Ⅱ)至多有1件次品的概率p=P(X=0)+P(X=1),由此能求出结果.
解答:
解:(Ⅰ)由题意知X=0,1,2,
P(X=0)=
=
=0.1,
P(X=1)=
=
=0.6,
P(X=2)=
=
=0.3,
∴取到的次品数X的分布列:
(Ⅱ)至多有1件次品的概率:
p=P(X=0)+P(X=1)=0.1+0.6=0.7.
P(X=0)=
| ||
|
| 1 |
| 10 |
P(X=1)=
| ||||
|
| 6 |
| 10 |
P(X=2)=
| ||
|
| 3 |
| 10 |
∴取到的次品数X的分布列:
| X | 0 | 1 | 2 |
| P | 0.1 | 0.6 | 0.3 |
p=P(X=0)+P(X=1)=0.1+0.6=0.7.
点评:本题考查概率的求法,考查离散型随机变量的分布列的求法,解题时要认真审题,是中档题.

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=
如图,在四棱锥P-ABCD中,底面四边形ABCD为矩形,PA=PD,AD=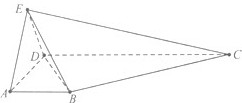 如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=
如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC= 如图,直三棱柱ABC-A1B1C1中,B1C1=A1C1,AC1⊥A1B,M,N分别是A1B1,AB的中点,求证:
如图,直三棱柱ABC-A1B1C1中,B1C1=A1C1,AC1⊥A1B,M,N分别是A1B1,AB的中点,求证: