题目内容
10.已知某企业的近3年的前7个月的月利润(单位:百万元)如下面的折线图所示: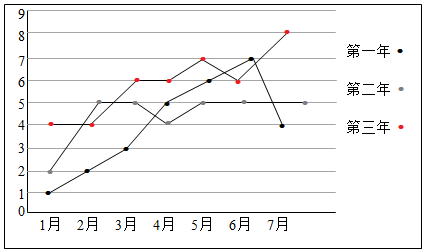
(1)试问这3年的前7个月中哪个月的月平均利润较高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
| 月份x | 1 | 2 | 3 | 4 |
| 利润y(单位:百万元) | 4 | 4 | 6 | 6 |
分析 (1)结合图象读出结论即可;(2)根据图象累加判断结论即可;(3)分别求出对应的系数$\widehat{a}$,$\widehat{b}$的值,代入回归方程即可.
解答 解:(1)由折线图可知5月和6月的平均利润最高.…(2分)
(2)第1年前7个月的总利润为1+2+3+5+6+7+4=28(百万元),…(3分)
第2年前7个月的总利润为2+5+5+4+5+5+5=31(百万元),…(4分)
第3年前7个月的总利润为4+4+6+6+7+6+8=41百万元),…(5分)
所以这3年的前7个月的总利润呈上升趋势.…(7分)
(3)∵$\overline x=2.5$,$\overline y=5,{1^2}+{2^2}+{3^2}+{4^2}=30$,1×4+2×4+3×6+4×6=54,
∴$\widehatb=\frac{54-4×2.5×5}{{30-4×{{2.5}^2}}}=0.8$,…(9分)
∴$\widehata=5-2.5×8=3$,…(10分)
∴$\widehaty=0.8x+3$,…(11分)
当x=8时,$\widehaty=0.8×8+3=9.4$(百万元),
∴估计8月份的利润为940万元.…(12分)
点评 本题考查了回归方程问题,考查折线图以及计算能力,是一道中档题.

练习册系列答案
相关题目
5.已知函数f(x)=aex-x(a∈R),其中e为自然对数的底数,e=2.71828…
(Ⅰ)判断函数f(x)的单调性,并说明理由
(Ⅱ)若x∈[1,2],不等式f(x)≥e-x恒成立,求a的取值范围.
(Ⅰ)判断函数f(x)的单调性,并说明理由
(Ⅱ)若x∈[1,2],不等式f(x)≥e-x恒成立,求a的取值范围.
15.下列函数既是奇函数又在定义域上单调递增的是( )
| A. | $f(x)=\frac{{{x^2}-2x}}{x-2}$ | B. | f(x)=x-$\frac{1}{x}$ | C. | f(x)=2x-2-x | D. | f(x)=x|sinx| |
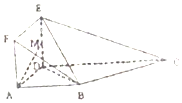 如图,在多面体ABCDEF中,平面ADEF与平面ABCD垂直,ADEF是正方形,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=$\frac{1}{2}$CD=1,M为线段ED的中点.
如图,在多面体ABCDEF中,平面ADEF与平面ABCD垂直,ADEF是正方形,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=$\frac{1}{2}$CD=1,M为线段ED的中点.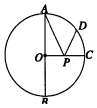 如图所示,AB为⊙O的直径,AB=2,OC是⊙O的半径,OC⊥AB,点D在$\widehat{AC}$上,$\widehat{AD}$=2$\widehat{CD}$,点P是OC上一动点,则PA+PD的最小值为$\sqrt{3}$.
如图所示,AB为⊙O的直径,AB=2,OC是⊙O的半径,OC⊥AB,点D在$\widehat{AC}$上,$\widehat{AD}$=2$\widehat{CD}$,点P是OC上一动点,则PA+PD的最小值为$\sqrt{3}$.