题目内容
13.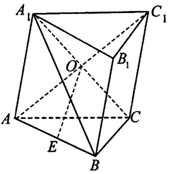 如图,在斜三梭柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1
如图,在斜三梭柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1(1)求证:E是AB中点;
(2)若AC1⊥A1B,求证:AC1⊥BC.
分析 (1)利用同一法,首先通过连接对角线得到中点,进一步利用中位线,得到线线平行,进一步利用线面平行的判定定理,得到结论.
(2)利用菱形的对角线互相垂直,进一步利用线面垂直的判定定理,得到线面垂直,最后转化成线线垂直.
解答 证明:(1)连结BC1, 取AB中点E′,
取AB中点E′,
∵侧面AA1C1C是菱形,AC1与A1C交于点O,
∴O为AC1的中点,
∵E′是AB的中点,
∴OE′∥BC1;
∵OE′?平面BCC1B1,BC1?平面BCC1B1,
∴OE′∥平面BCC1B1,
∵OE∥平面BCC1B1,
∴E,E′重合,
∴E是AB中点;
(2)∵侧面AA1C1C是菱形,
∴AC1⊥A1C,
∵AC1⊥A1B,A1C∩A1B=A1,A1C?平面A1BC,A1B?平面A1BC,
∴AC1⊥平面A1BC,
∵BC?平面A1BC,
∴AC1⊥BC.
点评 本题考查的知识要点:线面平行的判定定理,线面垂直的判定定理和性质定理,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列函数既是奇函数又在定义域上单调递增的是( )
| A. | $f(x)=\frac{{{x^2}-2x}}{x-2}$ | B. | f(x)=x-$\frac{1}{x}$ | C. | f(x)=2x-2-x | D. | f(x)=x|sinx| |
16. 如图,阴影部分的面积为( )
如图,阴影部分的面积为( )
 如图,阴影部分的面积为( )
如图,阴影部分的面积为( )| A. | 9 | B. | $\frac{9}{2}$ | C. | $\frac{13}{6}$ | D. | $\frac{7}{3}$ |

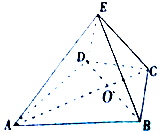 如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD.
如图,在四棱锥E-ABCD中,△ABD是正三角形,△BCD是等腰三角形,∠BCD=120°,EC⊥BD. 如图,在几何体A1B1D1-ABCD中,四边形A1B1BA与A1D1DA均为直角梯形,且AA1⊥底面ABCD,四边形ABCD为正方形,AB=2A1D1=2A1B1=4,AA1=4,P为DD1的中点.
如图,在几何体A1B1D1-ABCD中,四边形A1B1BA与A1D1DA均为直角梯形,且AA1⊥底面ABCD,四边形ABCD为正方形,AB=2A1D1=2A1B1=4,AA1=4,P为DD1的中点.