题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(Ⅰ)求椭圆C的方程;
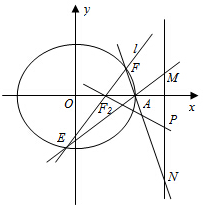
(Ⅱ)如图,过右焦点F2,且斜率为k(k≠0)的直线l与椭圆C相交于E、F两点,A为椭圆的右顶点,直线AE、AF分别交直线x=3于点M、N,线段MN的中点为P,记直线PF2的斜率为k′.求证:k•k′为定值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出b=
,a=
=2,由此能求出椭圆方程.
(Ⅱ)设过点F2(1,0)的直线l方程为:y=k(x-1),由
,得:(4k2+3)x2-8k2x+4k2-12=0,由已知条件利用韦达定理推导出直线PF2 的斜率k′=-
.由此能证明k•k′为定值-
.
| 3 |
| ||
| sin60° |
(Ⅱ)设过点F2(1,0)的直线l方程为:y=k(x-1),由
|
| 3 |
| 4k |
| 3 |
| 4 |
解答:
解:(Ⅰ)解:如图,∵椭圆C:
+
=1(a>b>0)的左右焦点分别为F1,F2,
点B(0,
)为短轴的一个端点,∠OF2B=60°,
∴b=
,a=
=
=2,…
故所求椭圆方程为
+
=1.…
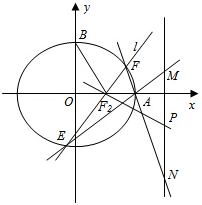 (Ⅱ)证明:设过点F2(1,0)的直线l方程为:y=k(x-1).…
(Ⅱ)证明:设过点F2(1,0)的直线l方程为:y=k(x-1).…
由
,
得:(4k2+3)x2-8k2x+4k2-12=0,…
因为点F2(1,0)在椭圆内,所以直线l和椭圆都相交,
即△>0恒成立.
设点E(x1,y1),F(x2,y2),则x1+x2=
,x1x2=
.…
因为直线AE的方程为:y=
(x-2),
直线AF的方程为:y=
(x-2),…
令x=3,得M(3,
),N(3,
),
所以点P的坐标(3,
(
+
)).…
直线PF2 的斜率为k′=
=
(
+
)
=
•
=
•
…
=
•
=-
.
所以k•k′为定值-
.…
| x2 |
| a2 |
| y2 |
| b2 |
点B(0,
| 3 |
∴b=
| 3 |
| b |
| sin∠OF2B |
| ||
| sin60° |
故所求椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
 (Ⅱ)证明:设过点F2(1,0)的直线l方程为:y=k(x-1).…
(Ⅱ)证明:设过点F2(1,0)的直线l方程为:y=k(x-1).…由
|
得:(4k2+3)x2-8k2x+4k2-12=0,…
因为点F2(1,0)在椭圆内,所以直线l和椭圆都相交,
即△>0恒成立.
设点E(x1,y1),F(x2,y2),则x1+x2=
| 8k2 |
| 4k2+3 |
| 4k2-12 |
| 4k2+3 |
因为直线AE的方程为:y=
| y1 |
| x1-2 |
直线AF的方程为:y=
| y2 |
| x2-2 |
令x=3,得M(3,
| y1 |
| x1-2 |
| y2 |
| x2-2 |
所以点P的坐标(3,
| 1 |
| 2 |
| y1 |
| x1-2 |
| y2 |
| x2-2 |
直线PF2 的斜率为k′=
| ||||||
| 3-1 |
=
| 1 |
| 4 |
| y1 |
| x1-2 |
| y2 |
| x2-2 |
=
| 1 |
| 4 |
| x1y2+x2y1-2(y1+y2) |
| x1x2-2(x1+x2)+4 |
=
| 1 |
| 4 |
| 2kx1x2-3k(x1+x2)+4k |
| x1x2-2(x1+x2)+4 |
=
| 1 |
| 4 |
2k•
| ||||
|
=-
| 3 |
| 4k |
所以k•k′为定值-
| 3 |
| 4 |
点评:本题考查椭圆方程的求法,考查两直线的斜率的乘积为定值的证明,解题时要认真审题,注意韦达定理的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知等差数列{an}的首项a1=1,公差d=2,则a4=( )
| A、5 | B、6 | C、7 | D、9 |
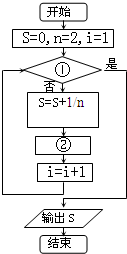
如图给出了计算
+
+
+…+
的值的程序框图,其中①②分别是( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 60 |

| A、i<30,n=n+2 |
| B、i=30,n=n+2 |
| C、i>30,n=n+2 |
| D、i>30,n=n+1 |