题目内容
设f（x）是可导函数，且f′（x0）=-3，
=（ ）
| lim |
| △x→0 |
| f(x0+△x)-f(x0-3△x) |
| △x |
| A、-3 | B、-6 | C、-9 | D、-12 |
考点：导数的运算
专题：导数的概念及应用
分析：根据导数的概念，将条件转化为f′（x0）的关系即可得到结论．
解答：
解：∵
=4×
=4f′（x0），
若f′（x0）=-3，
∴
=4f′（x0）=-3×4=-12，
故选：D．
| lim |
| △x→0 |
| f(x0+△x)-f(x0-3△x) |
| △x |
| lim |
| △x→0 |
| f(x0+△x)-f(x0-3△x) |
| 4△x |
若f′（x0）=-3，
∴
| lim |
| △x→0 |
| f(x0+△x)-f(x0-3△x) |
| △x |
故选：D．
点评：本题主要考查导数的概念，利用导数的概念将条件进行转化是解决本题的关键，比较基础．
练习册系列答案
相关题目
设x∈R，则“x＜
”是“2x2+x-1＜0”的（ ）
| 1 |
| 2 |
| A、充分必要条件 |
| B、充分但不必要条件 |
| C、必要但不充分条件 |
| D、既不充分也不必要条件 |
f（x）为一次函数，2f（2）-3f（1）=5，2f（0）-f（-1）=1，则f（x）的解析式为（ ）
| A、f（x）=3x+2 |
| B、f（x）=3x-2 |
| C、f（x）=2x+3 |
| D、f（x）=2x-3 |
Sn是等差数列{an}的前n项和，若S5=20，则a3=（ ）
| A、5 | B、6 | C、9 | D、4 |
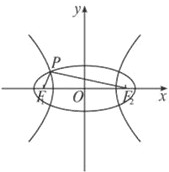如图，F1，F2是椭圆C1与双曲线C2的公共焦点，点P是椭圆和双曲线的一个交点，并且PF1⊥PF2，e1，e2分别是椭圆和双曲线的离心率，则（ ）| A、e1e2≥2 | ||||
| B、e12+e22≥4 | ||||
C、
| ||||
D、e1+e2≥2
|
若双曲线
-
=1（a＞0，b＞0）的右顶点为A，过其左焦点F作x轴的垂线交双曲线于M，N两点，且
•
＞0，则该双曲线离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| MA |
| NA |
| A、（2，+∞） | ||
| B、（1，2） | ||
C、（
| ||
D、（1，
|