题目内容
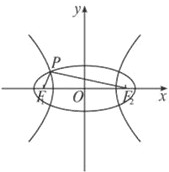如图，F1，F2是椭圆C1与双曲线C2的公共焦点，点P是椭圆和双曲线的一个交点，并且PF1⊥PF2，e1，e2分别是椭圆和双曲线的离心率，则（ ）| A、e1e2≥2 | ||||
| B、e12+e22≥4 | ||||
C、
| ||||
D、e1+e2≥2
|
考点：双曲线的简单性质,椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：设椭圆的方程为
+
=1，双曲线的方程为
-
=1，由题设条件，结合双曲线和椭圆的定义能推导出a2+m2=2c2，由此能求出结果．
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| m2 |
| y2 |
| n2 |
解答：
解：设椭圆的方程为
+
=1，
双曲线的方程为
-
=1，
则|PF1|+|PF2|=2a，∴|PF1|2+|PF2|2+2|PF1|•|PF2|=4a2，（1）
||PF1|-|PF2||=2m，∴|PF1|2+|PF2|2-2|PF1|•|PF2|=4m2，（2）
∵PF1⊥PF2，∴|PF1|2+|PF2|2=4c2，
[（1）+（2）]÷2，得
|PF1|2+|PF2|2=2a2+2m2=4c2，
∴a2+m2=2c2，
∴
+
=2，
∴
+
=2，
故选：C．
| x2 |
| a2 |
| y2 |
| b2 |
双曲线的方程为
| x2 |
| m2 |
| y2 |
| n2 |
则|PF1|+|PF2|=2a，∴|PF1|2+|PF2|2+2|PF1|•|PF2|=4a2，（1）
||PF1|-|PF2||=2m，∴|PF1|2+|PF2|2-2|PF1|•|PF2|=4m2，（2）
∵PF1⊥PF2，∴|PF1|2+|PF2|2=4c2，
[（1）+（2）]÷2，得
|PF1|2+|PF2|2=2a2+2m2=4c2，
∴a2+m2=2c2，
∴
| a2 |
| c2 |
| m2 |
| c2 |
∴
| 1 |
| e12 |
| 1 |
| e22 |
故选：C．
点评：本题考查双曲线和椭圆的离心率的性质，是中档题，解题时要认真审题，要熟练掌握双曲线、椭圆的简单性质．
练习册系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
设f（x）是可导函数，且f′（x0）=-3，
=（ ）
| lim |
| △x→0 |
| f(x0+△x)-f(x0-3△x) |
| △x |
| A、-3 | B、-6 | C、-9 | D、-12 |
已知平面内两个定点A（-1，0），B（1，0），过动点M作直线AB的垂线，垂足为N．若|MN|2=
•
，则动点M的轨迹是（ ）
| AN |
| BN |
| A、圆 | B、抛物线 | C、椭圆 | D、双曲线 |
已知直线l1：ax+2y-1=0与直线l2：ax-2y-3=0，“a=2”是“l1的方向向量是l2的法向量”的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
如果执行如图的框图，输入N=5，则输出的数等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，函数y=f（x）的图象在点P处的切线方程是y=-x+8，则f′（5）=（ ）
A、
| ||
| B、1 | ||
| C、-1 | ||
| D、0 |
如图，在三棱柱ABC-A1B1C1中，H是正方形AA1B1B的中心，AA1=2