题目内容
若双曲线
-
=1（a＞0，b＞0）的右顶点为A，过其左焦点F作x轴的垂线交双曲线于M，N两点，且
•
＞0，则该双曲线离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| MA |
| NA |
| A、（2，+∞） | ||
| B、（1，2） | ||
C、（
| ||
D、（1，
|
考点：双曲线的简单性质
专题：圆锥曲线中的最值与范围问题
分析：由已知条件，结合双曲线性质推导出|MF|=|NF|=
，|AF|=a+c，∠MAF＜45°，所以a+c＞
，由此能求出双曲线的离心率的取值范围．
| b2 |
| a |
| b2 |
| a |
解答：
解：如图，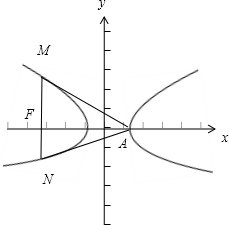
∵双曲线
-
=1（a＞0，b＞0）的右顶点为A，
过其左焦点F作x轴的垂线交双曲线于M，N两点，
∴|MF|=|NF|=
，|AF|=a+c，
∵
•
＞0，
∴∠MAF＜90°，
∵MN⊥AF，
∴∠MAF＜45°，
∴a+c＞
，
∴a2+ac＞b2=c2-a2，
∴e2-e-2＜0，
解得-1＜e＜2，
∵e＞1，∴1＜e＜2，
∴离心率的取值范围是（1，2）．
故选：B．
∵双曲线| x2 |
| a2 |
| y2 |
| b2 |
过其左焦点F作x轴的垂线交双曲线于M，N两点，
∴|MF|=|NF|=
| b2 |
| a |
∵
| MA |
| NA |
∴∠MAF＜90°，
∵MN⊥AF，
∴∠MAF＜45°，
∴a+c＞
| b2 |
| a |
∴a2+ac＞b2=c2-a2，
∴e2-e-2＜0，
解得-1＜e＜2，
∵e＞1，∴1＜e＜2，
∴离心率的取值范围是（1，2）．
故选：B．
点评：本题考查双曲线的离心率的取值范围的求法，是中档题，解题时要注意数形结合思想的合理运用．
练习册系列答案
相关题目
设f（x）是可导函数，且f′（x0）=-3，
=（ ）
| lim |
| △x→0 |
| f(x0+△x)-f(x0-3△x) |
| △x |
| A、-3 | B、-6 | C、-9 | D、-12 |
如果执行如图的框图，输入N=5，则输出的数等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，函数y=f（x）的图象在点P处的切线方程是y=-x+8，则f′（5）=（ ）
A、
| ||
| B、1 | ||
| C、-1 | ||
| D、0 |
已知方程组
对此方程组的每一组正实数解（x，y，z，u），其中z≥y，都存在正实数M，且满足M≤
，则M的最大值是（ ）
|
| z |
| y |
| A、1 | ||
B、3+2
| ||
C、6+4
| ||
D、3-2
|
椭圆有一个焦点固定，并通过两个已知点，且该焦点到这两个定点不等距．则该椭圆另一个焦点的轨迹类型是（ ）
| A、椭圆型 | B、双曲线型 |
| C、抛物线型 | D、非圆锥曲线型 |
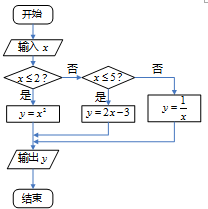给出了一个程序框图，其作用是输入x的值，输出相应的y的值，
如图，在三棱柱ABC-A1B1C1中，H是正方形AA1B1B的中心，AA1=2