题目内容
方程2cos
+1=0的解集是 .
| x |
| 2 |
考点:三角方程
专题:三角函数的求值
分析:由方程2cos
+1=0,化为cos
=-
,可得
=2kπ±
,即可得出.
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| 2π |
| 3 |
解答:
解:∵方程2cos
+1=0,
∴cos
=-
,
∴
=2kπ±
,即x=4kπ±
(k∈Z).
∴方程2cos
+1=0的解集是{x|x=4kπ±
(k∈Z)}.
故答案为:{x|x=4kπ±
(k∈Z)}.
| x |
| 2 |
∴cos
| x |
| 2 |
| 1 |
| 2 |
∴
| x |
| 2 |
| 2π |
| 3 |
| 4π |
| 3 |
∴方程2cos
| x |
| 2 |
| 4π |
| 3 |
故答案为:{x|x=4kπ±
| 4π |
| 3 |
点评:本题考查了三角方程的解法,属于基础题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
函数f(x)在定义域R上的导函数是f'(x),若f(x)=f(2-x),且当x∈(-∞,1)时,(x-1)f'(x)<0,设a=f(0)、b=f(
)、c=f(log28),则( )
| 2 |
| A、a<b<c |
| B、a>b>c |
| C、a<c<b |
| D、c<a<b |
若函数f(x)在[14,20]上连续,且同时满足f(14)•f(20)<0,f(14)•f(17)>0,则( )
| A、f(x)在[14,17]上有零点 |
| B、f(x)在[17,20]上有零点 |
| C、f(x)在[14,17]上无零点 |
| D、f(x)在[17,20]上无零点 |
设数列{an}的前n项和Sn=n2+n,则a7的值为( )
| A、13 | B、14 | C、15 | D、16 |
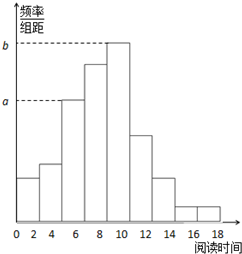 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图: