题目内容
ABCD是正方形,PA⊥平面AC,且PA=AB,则二面角B﹣PC﹣D的度数为( )
A.60° B.90° C.120° D.135°
C
【解析】
试题分析:通过建立如图所示的空间直角坐标系,利用两个平面的法向量的夹角求得二面角.
【解析】
由题意可得,AP,AB,AD两两垂直,所以可建立如图所示的空间直角坐标系.
则A(0,0,0),B(0,1,0),C(1,1,0),D(1,0,0),P(0,0,1).
∴ ,
, ,
, .
.
设平面PCD的法向量为 ,则
,则 得
得 ,
,
令x=1,则z=1,y=0.∴ .
.
同理可得平面PBC的法向量 =(0,1,1).
=(0,1,1).
∴ =
= =
= .
.
∴ .
.
从图中可以看到:二面角B﹣PC﹣D的大小应为一个钝角.
∴二面角B﹣PC﹣D的度数=180°﹣60°=120°.
故选C.


练习册系列答案
相关题目
 ,则B、C两点的球面距离是( )
,则B、C两点的球面距离是( )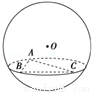
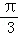 B.π C.
B.π C.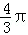 D.2π
D.2π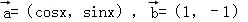 ,将函数
,将函数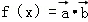 的图象按向量
的图象按向量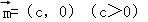 平移后,所得图象恰好为函数y=﹣f′(x)(f′(x)为f(x)的导函数)的图象,则c的值可以为( )
平移后,所得图象恰好为函数y=﹣f′(x)(f′(x)为f(x)的导函数)的图象,则c的值可以为( )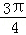 B.π C.
B.π C.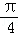 D.
D.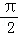
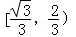 B.
B.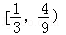 C.
C.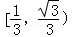 D.
D.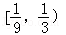
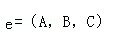 的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x﹣x0)+B(y﹣y0)+C(z﹣z0)=0”.如果给出平面α的方程是x﹣y+z=1,平面β的方程是
的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x﹣x0)+B(y﹣y0)+C(z﹣z0)=0”.如果给出平面α的方程是x﹣y+z=1,平面β的方程是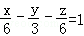 ,则由这两平面所成的二面角的正弦值是( )
,则由这两平面所成的二面角的正弦值是( )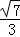 B.
B.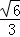 C.
C.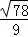 D.
D.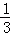
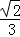 B.
B.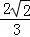 C.
C.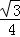 D.
D.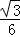
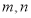 .
.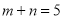 ”的概率;
”的概率;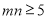 ”的概率.
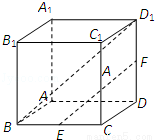
”的概率.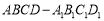 中,
中,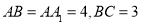 ,
,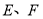 分别是所在棱
分别是所在棱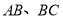 的中点,点
的中点,点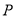 是棱
是棱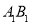 上的动点,联结
上的动点,联结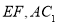 .如图所示.
.如图所示.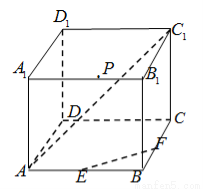
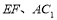 所成角的大小(用反三角函数值表示);
所成角的大小(用反三角函数值表示); 为顶点的三棱锥的体积.
为顶点的三棱锥的体积.