题目内容
在空间中,“经过点P(x0,y0,z0),法向量为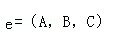 的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x﹣x0)+B(y﹣y0)+C(z﹣z0)=0”.如果给出平面α的方程是x﹣y+z=1,平面β的方程是
的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x﹣x0)+B(y﹣y0)+C(z﹣z0)=0”.如果给出平面α的方程是x﹣y+z=1,平面β的方程是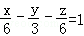 ,则由这两平面所成的二面角的正弦值是( )
,则由这两平面所成的二面角的正弦值是( )
A.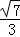 B.
B.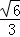 C.
C.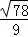 D.
D.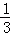
A
【解析】
试题分析:由定义得出两直线的法向量,数量积公式求出法向量的夹角余弦,利用同角三角函数的关系求出其正弦即可选出正确答案
【解析】
由题意,平面α,β的法向量分别是 ,
, ,
,
所以 ,
,
故选A

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 等于( )
等于( )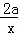 +3a,若f′(﹣1)=8,则f(﹣1)=( )
+3a,若f′(﹣1)=8,则f(﹣1)=( )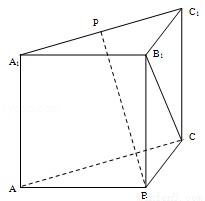
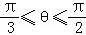 B.
B.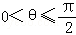 C.
C.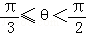 D.
D.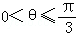
 ,
, ,则
,则 = .
= .
 是
是 所在平面上的两个定点,且满足
所在平面上的两个定点,且满足
 ,若
,若 ,则正实数
,则正实数 = .
= .