题目内容
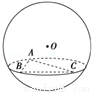
(2009•四川)如图,在半径为3的球面上有A、B、C三点,∠ABC=90°,BA=BC,球心O到平面ABC的距离是 ,则B、C两点的球面距离是( )
,则B、C两点的球面距离是( )
A.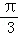 B.π C.
B.π C.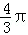 D.2π
D.2π
B
【解析】
试题分析:欲求B、C两点的球面距离,即要求出球心角∠BOC,将其置于三角形BOC中解决.
【解析】
∵AC是小圆的直径.
所以过球心O作小圆的垂线,垂足O′是AC的中点.
O′C= ,AC=3
,AC=3 ,
,
∴BC=3,即BC=OB=OC.∴ ,
,
则B、C两点的球面距离= .
.
故选B.

练习册系列答案
相关题目
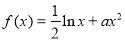
 .
.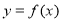 在点
在点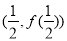 处的切线
处的切线 与直线
与直线 :
: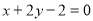 垂直,求
垂直,求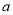 的值;
的值;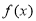 的单调性;若存在极值点
的单调性;若存在极值点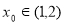 ,求实数
,求实数 的取值范围.
的取值范围. +1)R处有一点光源O,OA与球相切,则球在桌面上的投影——椭圆的离心率为 .
+1)R处有一点光源O,OA与球相切,则球在桌面上的投影——椭圆的离心率为 .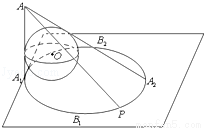
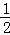 ;
;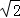 ;
;