题目内容
已知函数f(x)=x2-2ax+4b2,a,b∈R,若a从集合{3,4,5}中任取一个元素,b从集合{1,2,3}中任取一个元素,代入f(x)中形成函数.
(1)试列出所有的a与b的组合;
(2)求方程f(x)=0有两个不相等实根的概率.
(1)试列出所有的a与b的组合;
(2)求方程f(x)=0有两个不相等实根的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)列举出从a从集合{3,4,5}中任取和b从集合{1,2,3}中任取的基本事件个数,及满足条件方程y=0有两个不相等实根(△>0)的基本事件个数,代入古典概型概率计算公式,可得答案.
(2)根据古典概型的概率公式可得答案.
(2)根据古典概型的概率公式可得答案.
解答:
解:(Ⅰ)∵a取集合{3,4,5}中任一个元素,b取集合{1,2,3}中任一个元素,
∴a,b的取值的情况有(3,1),(3,2),(3,3),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3).其中第一个数表示a的取值,第二个数表示b的取值.…(6分)
(Ⅱ)设“方程f(x)=0有两个不相等的实根”为事件A,
当a>0,b>0时,方程f(x)=0有两个不相等实根的充要条件为a>2b.
当a>2b时,a,b取值的情况有(3,1),(4,1),(5,1),(5,2),
即A包含的基本事件数为4,而基本事件总数为9.
∴方程f(x)=0有两个不相等实根的概率P(A)=
…(13分)
∴a,b的取值的情况有(3,1),(3,2),(3,3),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3).其中第一个数表示a的取值,第二个数表示b的取值.…(6分)
(Ⅱ)设“方程f(x)=0有两个不相等的实根”为事件A,
当a>0,b>0时,方程f(x)=0有两个不相等实根的充要条件为a>2b.
当a>2b时,a,b取值的情况有(3,1),(4,1),(5,1),(5,2),
即A包含的基本事件数为4,而基本事件总数为9.
∴方程f(x)=0有两个不相等实根的概率P(A)=
| 4 |
| 9 |
点评:本题考查的知识点是几何概型,古典概型,其中分析出满足条件的基本事件的实质,方程y=0有两个不相等实根(△>0)与方程y=0没有实根(△<0)是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,在长方形ABCD中,AB=
,BC=1,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )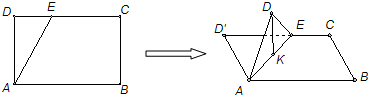
| 3 |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
数列1,3,6,10…的一个通项公式是( )
| A、an=n2-(n-1) | ||
B、an=
| ||
| C、an=n2-1 | ||
D、an=
|
用二分法求函数f(x)=ex-4x+1在区间(1,2)内零点的近似值的过程中得到f(15)<0,f(1.75)<0,f(1.875)>0,f(2)>0则函数零点落在区间( )
| A、(1.5,1.75) |
| B、(1.75,1.875) |
| C、(1.875,2) |
| D、不能确定 |
