题目内容
已知正三棱锥S-ABC的底面边长为4，高为3
（1）求正三棱锥S-ABC外接球半径；
（2）在正三棱锥内任取一点P，求点P满足VP-ABC＜
VS-ABC的概率．
（1）求正三棱锥S-ABC外接球半径；
（2）在正三棱锥内任取一点P，求点P满足VP-ABC＜
| 1 |
| 3 |
考点：几何概型,球的体积和表面积,球内接多面体
专题：计算题,概率与统计
分析：（1）由题意推出球心O到四个顶点的距离相等，利用勾股定理，求出球的半径，
（2）作出S在底面△ABC的射影为O，若VP-ABC=
VS-ABC，则高OP=
SO，所以概率为棱台与原棱锥体积之比，用相似比计算即可．
（2）作出S在底面△ABC的射影为O，若VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
解答：
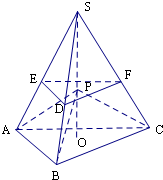解：（1）由题意，设正三棱锥S-ABC外接球半径为R，则
∵球心O到四个顶点的距离相等，正三棱锥S-ABC的底面边长为4，高为3，
∴R2=（
×4）2+（3-R）2，
∴外接球的半径为R=
；
（2）作出S在底面△ABC的射影为O，
若VP-ABC=
VS-ABC，则高OP=
SO，
∴VP-ABC＜
VS-ABC的概率P=1-（
）3=
．
解：（1）由题意，设正三棱锥S-ABC外接球半径为R，则∵球心O到四个顶点的距离相等，正三棱锥S-ABC的底面边长为4，高为3，
∴R2=（
| ||
| 3 |
∴外接球的半径为R=
| 43 |
| 18 |
（2）作出S在底面△ABC的射影为O，
若VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
∴VP-ABC＜
| 1 |
| 3 |
| 1 |
| 3 |
| 26 |
| 27 |
点评：本题是基础题，考查空间想象能力，计算能力；考查几何概型的概率计算，求出对应的体积关系是解决本题的关键，根据比例关系，得到面积之比是相似比的平方，体积之比是相似比的立方．
练习册系列答案
阅读快车系列答案
相关题目
如图，在四棱锥S-ABCD中，SA⊥平面ABCD，底ABCD为正方形，M、N分别为SB、SD的中点．求证：
如图是一个组合体的三视图（单位：cm），
已知向量