题目内容
如图是一个组合体的三视图（单位：cm），（1）此组合体是由上下两个几何体组成，试说出上下两个几何体的名称，并用斜二测画法画出下半部分几何体的直观图；
（2）求这个组合体的体积．
考点：棱柱、棱锥、棱台的体积,简单空间图形的三视图
专题：空间位置关系与距离
分析：（1）由组合体的三视图知该组合体的上部分是直径为6cm的球，下部分是上底边长为6cm，下底边长为10cm、高为8cm的正四棱台．由此能作出这个几何体的直观图．
（2）分别求出球和四棱台的体积，由此能求出这个组合体的体积．
（2）分别求出球和四棱台的体积，由此能求出这个组合体的体积．
解答：
解：（1）由组合体的三视图知：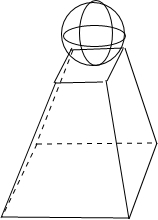
该组合体的上部分是直径为6cm的球，
下部分是上底边长为6cm，下底边长为10cm、高为8cm的正四棱台．四棱台…（2分）
这个几何体的直观图如右图所示．…（6分）
（2）V球=
×πR3=36π(cm3)…（8分）
V台=
(S+S′+
)h
=
(100+36+
)×8=
（cm3）…（11分）
∴这个组合体的体积：
V=
+36π（cm3）…（12分）
该组合体的上部分是直径为6cm的球，
下部分是上底边长为6cm，下底边长为10cm、高为8cm的正四棱台．四棱台…（2分）
这个几何体的直观图如右图所示．…（6分）
（2）V球=
| 1 |
| 3 |
V台=
| 1 |
| 3 |
| SS′ |
=
| 1 |
| 3 |
| 100×36 |
| 1568 |
| 3 |
∴这个组合体的体积：
V=
| 1568 |
| 3 |
点评：本题考查几何体名称和直观图的求法，考查组合体的体积的求法，解题时要认真审题，注意棱台的体积公式的合理运用．
练习册系列答案
相关题目
如图，直三棱柱ABC-A1B1C1中，D、E分别是AB，BB1的中点．
如图，平行六面体ABCD-A1B1C1D1中，底面ABCD是边长为1的正方形，AA1=