题目内容
14．已知抛物线的顶点在原点，焦点在y轴上，抛物线上的点P（m，-2）到焦点的距离为5，则m的值为（ ）| A． | ±4 | B． | ±2$\sqrt{5}$ | C． | ±2$\sqrt{6}$ | D． | ±5 |
分析 利用抛物线的性质，求出抛物线的焦点坐标，转化求解即可．
解答 解：抛物线的顶点在原点，焦点在y轴上，抛物线上的点P（m，-2），
可知抛物线的开口向下，抛物线上的点P（m，-2）到焦点的距离为5，
可得准线方程为：y=3，焦点坐标（0，-3），
则：$\sqrt{{m}^{2}+{1}^{2}}$=5，解得m=±2$\sqrt{6}$．
故选：C．
点评 本题考查抛物线的简单性质的应用，考查计算能力．
练习册系列答案
相关题目
1．观察下列事实：|x|+|y|=1的不同整数解（x，y）的个数为4，|x|+|y|=2的不同整数解（x，y）的个数为8，|x|+|y|=3的不同整数解（x，y）的个数为12，…，则|x|+|y|=100的不同整数解（x，y）的个数为（ ）
| A． | 400 | B． | 420 | C． | 440 | D． | 480 |
在平面直角坐标系中，已知两定点$A（-\frac{1}{3}\;，\;0）$和$B（{\frac{1}{3}\;，\;0}）$，点M是平面内的动点，且$|{\overrightarrow{AB}+\overrightarrow{AM}}|+|{\overrightarrow{BA}+\overrightarrow{BM}}|=4$．
6．用数学归纳法证明f（x）=1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{n}-1}$＞$\frac{n}{2}$（n∈N*）的过程中，假设当n=k时成立，则当n=k+1时，左边f（k+1）=（ ）
| A． | f（k）+$\frac{1}{{2}^{k+1}-1}$ | |
| B． | f（k）+$\frac{1}{{2}^{k+1}}$ | |
| C． | f（k）+$\frac{1}{{2}^{k}-1}$+$\frac{1}{{2}^{k}}$+$\frac{1}{{2}^{k}+1}$+…+$\frac{1}{{2}^{k+1}-1}$ | |
| D． | f（k）+$\frac{1}{{2}^{k}}$+$\frac{1}{{2}^{k}+1}$+…+$\frac{1}{{2}^{k+1}-1}$ |
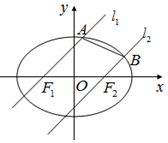已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左、右焦点分别为F1、F2，离心率为$\frac{1}{2}$，直线y=1与C的两个交点间的距离为$\frac{{4\sqrt{6}}}{3}$．
如图所示，Rt△ABC的顶点A坐标（-2，0），直角顶点B（0，-2$\sqrt{2}$），顶点C在x轴上，点P为线段OA的中点．