题目内容
（1）已知sin
-cos
=
，求sinα的值；
（2）已知α，β都是锐角，tanα=
，tanβ=
，求tan（α+2β）的值．
| α |
| 2 |
| α |
| 2 |
| 1 |
| 5 |
（2）已知α，β都是锐角，tanα=
| 1 |
| 7 |
| 1 |
| 3 |
考点：两角和与差的正切函数,同角三角函数基本关系的运用
专题：三角函数的求值
分析：（1）把所给的等式平方，利用同角三角函数的基本关系求得sinα的值．
（2）由条件求得tan2β的值，再利用两角和的正切公式求得tan（α+2β）的值．
（2）由条件求得tan2β的值，再利用两角和的正切公式求得tan（α+2β）的值．
解答：
解：（1）∵(sin
-cos
)2=1-sinα=
∴sinα=
．
（2）∵tan2β=
=
，∴tan(α+2β)=
=
=1．
| α |
| 2 |
| α |
| 2 |
| 1 |
| 25 |
| 24 |
| 25 |
（2）∵tan2β=
| 2tanβ |
| 1-tan2β |
| 3 |
| 4 |
| tanα+tan2β |
| 1-tanα•tan2β |
| ||||
1-
|
点评：本题主要考查了同角三角函数的基本关系，正弦的二倍角公式，正切的和角、倍角公式，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
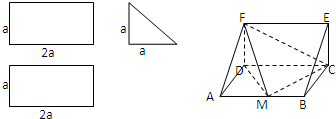一个多面体的三视图和直观图如图所示，其中正视图和俯视图均为矩形，侧视图为直角三角形，M是AB的中点．
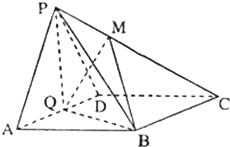如图，四棱锥P-ABCD中，四边形ABCD为平行四边形，面PAD⊥平面ABCD，PA=PD，Q为AD的中点，且QB⊥AD．