题目内容
已知圆C:x2+y2-2x+4y-4=0,一条斜率等于1的直线l与圆C交于A,B两点.
(1)求弦AB最长时直线l的方程;
(2)求△ABC面积最大时直线l的方程.
(1)求弦AB最长时直线l的方程;
(2)求△ABC面积最大时直线l的方程.
考点:直线与圆的位置关系
专题:直线与圆
分析:(1)欲求弦AB最长时直线L的方程,依据圆的特征:圆的直径是最长的弦,只须求出l过圆心时的方程即可;
(2)欲求△ABC面积最大时直线L的方程,因其两腰定长,故只须顶角为直角时面积最大,最后利用点到直线的距离公式求解即可;
(2)欲求△ABC面积最大时直线L的方程,因其两腰定长,故只须顶角为直角时面积最大,最后利用点到直线的距离公式求解即可;
解答:
解:(1)∵L过圆心时弦长AB最大,圆心坐标为(1,-2),∴L的方程为x-y-3=0(4分)
(2)△ABC的面积S=
CA•CBsin∠ACB=
sin∠ACB,
当∠ACB=
时,△ABC的面积S最大,
此时△ABC为等腰三角形;
设L方程为y=x+m,则圆心到直线距离为
,
从而有
=
,
m=0或m=-6,
则L方程为x-y=0或x-y-6=0(8分).
(2)△ABC的面积S=
| 1 |
| 2 |
| 9 |
| 2 |
当∠ACB=
| π |
| 2 |
此时△ABC为等腰三角形;
设L方程为y=x+m,则圆心到直线距离为
3
| ||
| 2 |
从而有
| |1+2+m| | ||
|
3
| ||
| 2 |
m=0或m=-6,
则L方程为x-y=0或x-y-6=0(8分).
点评:本小题主要考查直线的一般式方程、直线和圆的方程的应用、点到直线的距离公式等基础知识,考查运算求解能力,考查数形结合思想、函数与方程思想、化归与转化思想.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题中,正确的是( )
| A、若三条直线两两平行,则这三条直线必共面 |
| B、互不平行的两条直线是异面直线 |
| C、分别位于两个不同平面内的两条直线是异面直线 |
| D、不同在任何一个平面内的两条直线是异面直线 |
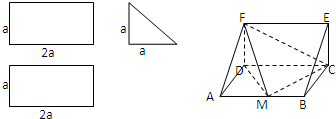 一个多面体的三视图和直观图如图所示,其中正视图和俯视图均为矩形,侧视图为直角三角形,M是AB的中点.
一个多面体的三视图和直观图如图所示,其中正视图和俯视图均为矩形,侧视图为直角三角形,M是AB的中点.
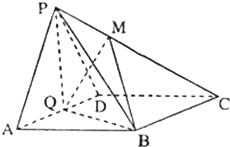 如图,四棱锥P-ABCD中,四边形ABCD为平行四边形,面PAD⊥平面ABCD,PA=PD,Q为AD的中点,且QB⊥AD.
如图,四棱锥P-ABCD中,四边形ABCD为平行四边形,面PAD⊥平面ABCD,PA=PD,Q为AD的中点,且QB⊥AD.