题目内容
函数y=
的值域是 ．
2-
| ||
| 3-x |
考点：函数的值域
专题：函数的性质及应用
分析：令x=cosx，则
=|sinx|，则y=
=
，函数y值表示动点（cosx，|sinx|）与定点P（3，2）连线的斜率k，然后数形结合求出y的最值，进而可得函数的值域．
| 1-x2 |
2-
| ||
| 3-x |
| 2-|sinx| |
| 3-cosx |
解答：
解：令x=cosx，则
=|sinx|，
则y=
=
，
函数y值表示动点（cosx，|sinx|）与定点P（3，2）连线的斜率k，
由下图可得：
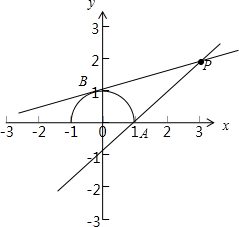
当直线过A（1，0）时，k取最大值1，
当直线与半圆相切时，k取最小值，
此时
=1，
解得k=
，或k=
（舍去），
故函数y=
的值域是[
，1]，
故答案为：[
，1]
| 1-x2 |
则y=
2-
| ||
| 3-x |
| 2-|sinx| |
| 3-cosx |
函数y值表示动点（cosx，|sinx|）与定点P（3，2）连线的斜率k，
由下图可得：
当直线过A（1，0）时，k取最大值1，
当直线与半圆相切时，k取最小值，
此时
| |2-3k| | ||
|
解得k=
3-
| ||
| 4 |
3+
| ||
| 4 |
故函数y=
2-
| ||
| 3-x |
3-
| ||
| 4 |
故答案为：[
3-
| ||
| 4 |
点评：本题考查的知识点是函数的值域，其中根据已知分析出函数的值y表示动点（cosx，|sinx|）与定点P（3，2）连线的斜率k，是解答的关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
已知x∈[0，2π]，如果y=cosx是减函数，且y=sinx是增函数，那么（ ）
A、0≤x≤
| ||
B、
| ||
C、π≤x≤
| ||
D、
|
