题目内容
sin2x-sinxcosx+2cos2x= .
考点:二倍角的正弦,二倍角的余弦
专题:计算题,三角函数的求值
分析:利用二倍角公式,结合辅助角公式,即可得出结论.
解答:
解:sin2x-sinxcosx+2cos2x=
-
+2•
=
+
(cos2x-sin2x)
=
+
cos(2x+
).
故答案为:
+
cos(2x+
).
| 1-cos2x |
| 2 |
| sin2x |
| 2 |
| 1+cos2x |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
| ||
| 2 |
| π |
| 4 |
故答案为:
| 3 |
| 2 |
| ||
| 2 |
| π |
| 4 |
点评:本题考查二倍角公式、辅助角公式,考查学生的计算能力,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
下列说法正确的是( )
A、若a∈R,则“
| ||
| B、“p∧q为真命题”是“p∨q为真命题”的必要不充分条件 | ||
C、若命题p:“?x∈R,sinx+cosx≤
| ||
| D、命题“?x0∈R,使得x02+2x0+3<0”的否定是“?x∈R,x2+2x+3>0” |
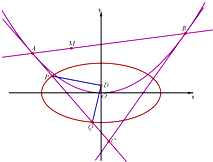 已知抛物线C2:x2=2py(p>0)的通径长为4,椭圆C1:
已知抛物线C2:x2=2py(p>0)的通径长为4,椭圆C1: