题目内容
下列从集合A到集合B的对应中是映射的有 ；其中一一映射的有 ．
①A=N*，B={0，1，2，3，4}，f：除以5的余数；
②A={x|x≥0}，B={y|y≥0}，f：x→y=
；
③A=N*，B={-1，1，2，-2}，f：x→（-1）x
④A=Z，B=R，f：x→
⑤A=N*，B=R，f：x→
⑥A={平面α内的圆}，B={平面α内的矩形}，f：A中圆的内接矩形．
①A=N*，B={0，1，2，3，4}，f：除以5的余数；
②A={x|x≥0}，B={y|y≥0}，f：x→y=
| x |
③A=N*，B={-1，1，2，-2}，f：x→（-1）x
④A=Z，B=R，f：x→
| 2 |
| x |
⑤A=N*，B=R，f：x→
| x2 |
⑥A={平面α内的圆}，B={平面α内的矩形}，f：A中圆的内接矩形．
考点：映射
专题：函数的性质及应用
分析：根据映射、一一映射的定义，判断各个选项中的对应是否是映射、是否是一一映射，从而得出结论．
解答：
解：①A中元素，按照f：除以5的余数，在B中均有唯一的相，故①中对应是从集合A到集合B的映射；
但B中元素在A中的原相不唯一，故①中对应不是从集合A到集合B的一一映射；
②A中元素，按照f：x→y=
，在B中均有唯一的相，故②中对应是从集合A到集合B的映射；
且B中元素在A中的原相也是唯一的，故②中对应是从集合A到集合B的一一映射；
③A中元素，按照f：x→（-1）x，在B中均有唯一的相，故③中对应是从集合A到集合B的映射；
但B中元素在A中的原相不唯一，故③中对应不是从集合A到集合B的一一映射；
④A中元素0，按照f：x→
没有对应的相，故④中对应不是从集合A到集合B的映射；
⑤A中元素，按照f：x→
，在B中均有唯一的相，故⑤中对应是从集合A到集合B的映射；
但B中元素在A中的不一定找到原相，故⑤中对应不是从集合A到集合B的一一映射；
⑥A中元素，按照f：A中圆的内接矩形，在B中对应的相有无限多个，故⑥中对应不是从集合A到集合B的映射；
故从集合A到集合B的对应中是映射的有：①②③⑤，其中一一映射有：②，
故答案为：①②③⑤，②
但B中元素在A中的原相不唯一，故①中对应不是从集合A到集合B的一一映射；
②A中元素，按照f：x→y=
| x |
且B中元素在A中的原相也是唯一的，故②中对应是从集合A到集合B的一一映射；
③A中元素，按照f：x→（-1）x，在B中均有唯一的相，故③中对应是从集合A到集合B的映射；
但B中元素在A中的原相不唯一，故③中对应不是从集合A到集合B的一一映射；
④A中元素0，按照f：x→
| 2 |
| x |
⑤A中元素，按照f：x→
| x2 |
但B中元素在A中的不一定找到原相，故⑤中对应不是从集合A到集合B的一一映射；
⑥A中元素，按照f：A中圆的内接矩形，在B中对应的相有无限多个，故⑥中对应不是从集合A到集合B的映射；
故从集合A到集合B的对应中是映射的有：①②③⑤，其中一一映射有：②，
故答案为：①②③⑤，②
点评：本题主要考查映射、一一映射的定义，属于基础题．
练习册系列答案
相关题目
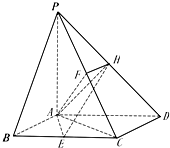如图，四棱锥P-ABCD的底面是菱形，∠ABC=60°，PA⊥底面ABCD，E，F分别是BC，PC的中点，点H在PD上，且EH⊥PD，PA=AB=2．
