题目内容
18.已知数列{an}中,a1=1,an+1+an=-2n,求:an.分析 由已知数列递推式可得an+an-1=-2(n-1)(n≥2),进一步可得数列{an}的奇数项是以1为首项,以-2为公差的等差数列;偶数项是以-3为首项,以-2为公差的等差数列.由此可得数列的通项公式.
解答 解:由an+1+an=-2n,
得an+an-1=-2(n-1)(n≥2),
两式作差得:an+1-an-1=-2(n≥2),
又由a1=1,an+1+an=-2n,
得a2=-2-a1=-3,
∴数列{an}的奇数项是以1为首项,以-2为公差的等差数列;
偶数项是以-3为首项,以-2为公差的等差数列.
则${a}_{n}=\left\{\begin{array}{l}{-n+2,n为奇数}\\{-n-1,n为偶数}\end{array}\right.$.
点评 本题考查数列递推式,考查了等差关系的确定,关键是掌握奇数项和偶数项分别成等差数列的通项公式的求法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.方程y一1=$\sqrt{1-{x}^{2}}$表示的曲线是( )
| A. | 直线 | B. | 射线 | C. | 圆 | D. | 半圆 |
6.已知某几何体的三视图如图所示,则该几何体的体积是( )
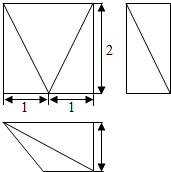

| A. | 2 | B. | 4 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
3.抛物线的顶点在原点,焦点在x轴上,其通径的两端与顶点连成的三角形的面积为4.则此抛物线的方程是( )
| A. | y2=8$\sqrt{2}$x | B. | y2=±4$\sqrt{2}$x | C. | y2=±4x | D. | y2=±8$\sqrt{2}$x |