题目内容
16.有4名男生、5名女生,全体排成一行,问下列情形各有多少种不同的排法?(1)一共有多少种排法?
(2)甲不在中间;
(3)甲、乙两人必须排在两端;
(4)男女相间.
分析 (1)9人全排共有A99种排法;
(2)这是一个排列问题,一般情况下,我们会从受到限制的特殊元素开始考虑,先排甲有8种,剩下的8个元素全排列有A88种,根据分步计数原理得到结果.
(3)先排甲、乙,再排其余7人,再根据分步计数原理得到结果.
(4)先排4名男生有A44种方法,再将5名女生插在男生形成的5个空上有A55种方法,根据分步计数原理得到结果.
解答 解:(1)9人共有A99种排法;
(2)先排甲有8种,其余有A88种,
∴共有8•A88种排法.
(3)先排甲、乙,再排其余7人,共有A22•A77=10080种排法.
(4)先排4名男生有A44种方法,再将5名女生插在男生形成的5个空上有A55种方法,
故共有A44•A55=2880种排法.
点评 排列问题常见的解题思路:元素分析法(优先考虑特殊元素)、位置分析法(优先考虑特殊位置)、直接法、间接法(排除法)、捆绑法、等机会法、插空法等常见的解题思路.

练习册系列答案
相关题目
6.已知某几何体的三视图如图所示,则该几何体的体积是( )
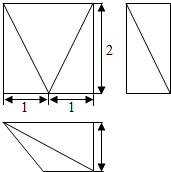

| A. | 2 | B. | 4 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
11.设等比数列{an}的前n项和为Sn,若S7=S9=2,则a8等于( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
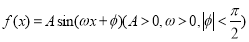 的部分图象如图所示.
的部分图象如图所示.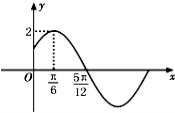
 ,
,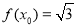 ,若g(x)=1+2cos2x,求g(x0)的值;
,若g(x)=1+2cos2x,求g(x0)的值; 上有解,求实数a的取值范围.
上有解,求实数a的取值范围.