题目内容
有甲、乙、丙、丁、戊5位同学,求:
(1)5位同学站成一排,有多少种不同的方法?
(2)5位同学站成一排,要求甲乙必须相邻,丙丁不能相邻,有多少种不同的方法?
(3)将5位同学分配到三个班,每班至少一人,共有多少种不同的分配方法?
(1)5位同学站成一排,有多少种不同的方法?
(2)5位同学站成一排,要求甲乙必须相邻,丙丁不能相邻,有多少种不同的方法?
(3)将5位同学分配到三个班,每班至少一人,共有多少种不同的分配方法?
考点:计数原理的应用
专题:排列组合
分析:(1)5位同学站成一排,全排列即可.
(2)利用捆绑和插空法排列即可.
(3)分组(3,1,1),(2,2,1)两组,计算即可.
(2)利用捆绑和插空法排列即可.
(3)分组(3,1,1),(2,2,1)两组,计算即可.
解答:
解:(1)5位同学站成一排共有
=120.
(2)5位同学站成一排,要求甲乙必须相邻,丙丁不能相邻,先用捆绑排甲乙,再和戊全排,形成3个空,插入丙丁即可.
故有
•
•
=24.
(3)人数分配方式有①3,1,1有
•
=60种方法
②2,2,1有
•
=90种方法
所以,所有方法总数为60+90=150种方法.
| A | 5 5 |
(2)5位同学站成一排,要求甲乙必须相邻,丙丁不能相邻,先用捆绑排甲乙,再和戊全排,形成3个空,插入丙丁即可.
故有
| A | 2 2 |
| A | 2 2 |
| A | 2 3 |
(3)人数分配方式有①3,1,1有
| C | 3 5 |
| A | 3 3 |
②2,2,1有
| ||||
|
| A | 3 3 |
所以,所有方法总数为60+90=150种方法.
点评:本题考查排列、组合的应用,(1)中注意优先分析特殊元素,(2)运用捆绑法与插空法来分析相邻与不相邻问题,(3)注意分类讨论的应用.

练习册系列答案
相关题目
 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=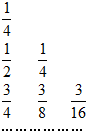 下表给出一个“三角形数阵”(如图),已知每一列的数成等差数列,从第三行起每一行的公比都相等,记第i行第j列的数为aij(i≥j,i,j∈N*).
下表给出一个“三角形数阵”(如图),已知每一列的数成等差数列,从第三行起每一行的公比都相等,记第i行第j列的数为aij(i≥j,i,j∈N*). 在三棱锥S-ABC中,△ABC是边长为8的正三角形,SA=SC=2
在三棱锥S-ABC中,△ABC是边长为8的正三角形,SA=SC=2