题目内容
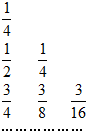 下表给出一个“三角形数阵”(如图),已知每一列的数成等差数列,从第三行起每一行的公比都相等,记第i行第j列的数为aij(i≥j,i,j∈N*).
下表给出一个“三角形数阵”(如图),已知每一列的数成等差数列,从第三行起每一行的公比都相等,记第i行第j列的数为aij(i≥j,i,j∈N*).(1)求a83;
(2)试写出aij关于i,j的关系式;
(3)记第n行的和An,求数列{An}的前m项和Bm的表达式.
考点:数列的求和,进行简单的合情推理
专题:综合题,等差数列与等比数列
分析:(1)求出第一列的公差,利用等差数列的通项公式求a83;
(2)利用等比数列的性质写出aij;
(3)先表示出An,Bm,然后利用错位相减法求出数阵中所有数之和.
(2)利用等比数列的性质写出aij;
(3)先表示出An,Bm,然后利用错位相减法求出数阵中所有数之和.
解答:
解:(1)由题意知,第一列公差为d=
-
=
,每行成等比数列,且公比q=
,
由已知a81=
+(8-1)×
=2,
又a83是第8行第3个数,
故a83=a81•q2=
;
(Ⅱ)∵ai1=
+(i-1)×
=
,
∴aij=
.(
)j-1.
(Ⅲ)设数阵中第n行的所有数字之和为An,
则An=
(1+
+…+
)=
-
×
.
所求之和Bm=A1+A2+…+Am=
(1+2+…+m)-
(1×
+2×
+…+m•
).
设S=1×
+2×
+…+m•
,
则
S=1×
+…+(m-1)•
+m•
,
两式相减得
S=
+
+…+
-
=
-
=1-
,
∴Bm=
-(1-
).
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
由已知a81=
| 1 |
| 4 |
| 1 |
| 4 |
又a83是第8行第3个数,
故a83=a81•q2=
| 1 |
| 2 |
(Ⅱ)∵ai1=
| 1 |
| 4 |
| 1 |
| 4 |
| i |
| 4 |
∴aij=
| i |
| 4 |
| 1 |
| 2 |
(Ⅲ)设数阵中第n行的所有数字之和为An,
则An=
| n |
| 4 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| n |
| 2 |
| 1 |
| 2 |
| n |
| 2n |
所求之和Bm=A1+A2+…+Am=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2m |
设S=1×
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2m |
则
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2m |
| 1 |
| 2m+1 |
两式相减得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2m |
| m |
| 2m+1 |
| ||||
1-
|
| m |
| 2m+1 |
| 2+m |
| 2m+1 |
∴Bm=
| m(m+1) |
| 4 |
| 2+m |
| 2m+1 |
点评:本题主要考查了等差数列和等比数列的综合运用,运算量较大,综合性较强,考查学生的运算能力.

练习册系列答案
相关题目