题目内容
已知二项式(
-
)n的展开式的二项式系数和为128.
(1)求n的值;
(2)求该二项展开式的各项的系数和;
(3)求该二项展开式的一次项.
| x |
| 2 | |||
|
(1)求n的值;
(2)求该二项展开式的各项的系数和;
(3)求该二项展开式的一次项.
考点:二项式系数的性质
专题:二项式定理
分析:(1)根据展开式的二项式系数和为2n=128,求得n的值.
(2)在二项式(
-
)n的展开式中,令x=1得,该二项展开式的各项系数和.
(3)先求出二项式展开式的通项公式,再令x的幂指数等于1,求得r的值,即可求得展开式中展开式的一次项
(2)在二项式(
| x |
| 2 | |||
|
(3)先求出二项式展开式的通项公式,再令x的幂指数等于1,求得r的值,即可求得展开式中展开式的一次项
解答:
解:(1)由题意2n=128,∴n=7.
(2)在二项式(
-
)n的展开式中,令x=1得,该二项展开式的各项系数和(1-2)7=-1.
3)设该二项展开式的第r+1项为Tr+1,则Tr+1=
x
•(-2)rx-
=(-2)r
x
.
令
=1得r=3,可得 T4=(-2)3
x=-280x.
即所求一次项为-280x.
(2)在二项式(
| x |
| 2 | |||
|
3)设该二项展开式的第r+1项为Tr+1,则Tr+1=
| C | r 7 |
| 7-r |
| 2 |
| r |
| 3 |
| C | r 7 |
| 21-5r |
| 6 |
令
| 21-5r |
| 6 |
| C | 3 7 |
即所求一次项为-280x.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,注意各项系数和与各项的二项式系数和的区别,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
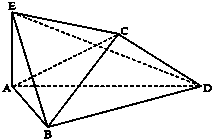 菱形ABCD边长为2,∠BAD=60°,将ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=
菱形ABCD边长为2,∠BAD=60°,将ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=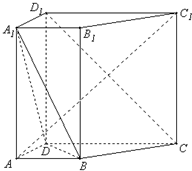 如图,在直四棱柱ANCD-A1B1C1D1中,已知DC=DD1=2AD=2AB=2,AD⊥DC,AB∥DC.
如图,在直四棱柱ANCD-A1B1C1D1中,已知DC=DD1=2AD=2AB=2,AD⊥DC,AB∥DC.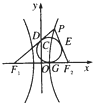 如图所示,已知P为双曲线
如图所示,已知P为双曲线