题目内容
 在三棱锥S-ABC中,△ABC是边长为8的正三角形,SA=SC=2
在三棱锥S-ABC中,△ABC是边长为8的正三角形,SA=SC=2| 7 |
(1)求证:AC⊥SB;
(2)求三棱锥S-ABC的体积;
(3)求二面角S-BC-A的正切值.
考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(1)取AC的中点D,连接SD,BD,证明SD⊥AC,BD⊥AC,说明AC⊥面SBD,即可证明AC⊥SB.
(2)过S作SO⊥BD于O,说明∠SDB为二面角S-AC-B平面角,求出SO,然后求出几何体的体积.
(3)过O作OH⊥BC于H,连SH,则SH⊥BC,所以∠SHO为二面角S-BC-A的平面角,分别在三角形中求相应线段的长,从而可解.
(2)过S作SO⊥BD于O,说明∠SDB为二面角S-AC-B平面角,求出SO,然后求出几何体的体积.
(3)过O作OH⊥BC于H,连SH,则SH⊥BC,所以∠SHO为二面角S-BC-A的平面角,分别在三角形中求相应线段的长,从而可解.
解答:
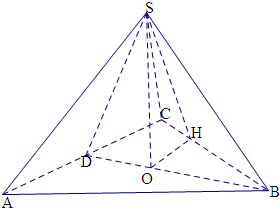 解(1)取AC的中点D,连接SD,BD,
解(1)取AC的中点D,连接SD,BD,
∵SA=SC,D为AC的中点,
∴SD⊥AC,∵AB=BC,D为AC的中点,
∴BD⊥AC,又SD∩BD=D∴AC⊥面SBD,
又SB?面SBD,∴AC⊥SB;
(2)过S作SO⊥BD于O,∵AC⊥面SBD,
又AC?平面ABC∴平面SBD⊥平面ABC,
又SO⊥BD∴SO⊥平面ABC,
在Rt△SAD中,SA=2
,AD=
AC=4
∴SD=
=2
∵SD⊥AC,BD⊥AC,∴∠SDB为二面角S-AC-B平面角,∴∠SDB=60°,
在Rt△SDO中,SOSO=SDsin∠SDO=2
×
=3,
∴VS-ABC=
S△ABC•SO=
•
•64•3=16
;
(3)过O作OH⊥BC于H,连SH,则SH⊥BC∴∠SHO为二面角S-BC-A的平面角
∵正△ABC是边长为8,∴BD=4
,∵OD=
=
,∴OB=3
,
在Rt△OHB中,OH=OBsin30°=
OB=
,在Rt△SOH中,tan∠SHO=
=
=
.
即二面角S-BC-A的正切值为
.
 解(1)取AC的中点D,连接SD,BD,
解(1)取AC的中点D,连接SD,BD,∵SA=SC,D为AC的中点,
∴SD⊥AC,∵AB=BC,D为AC的中点,
∴BD⊥AC,又SD∩BD=D∴AC⊥面SBD,
又SB?面SBD,∴AC⊥SB;
(2)过S作SO⊥BD于O,∵AC⊥面SBD,
又AC?平面ABC∴平面SBD⊥平面ABC,
又SO⊥BD∴SO⊥平面ABC,
在Rt△SAD中,SA=2
| 7 |
| 1 |
| 2 |
∴SD=
| 28-16 |
| 3 |
在Rt△SDO中,SOSO=SDsin∠SDO=2
| 3 |
| ||
| 2 |
∴VS-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| 3 |
(3)过O作OH⊥BC于H,连SH,则SH⊥BC∴∠SHO为二面角S-BC-A的平面角
∵正△ABC是边长为8,∴BD=4
| 3 |
| SD2-SO2 |
| 3 |
| 3 |
在Rt△OHB中,OH=OBsin30°=
| 1 |
| 2 |
3
| ||
| 2 |
| SO |
| OH |
| 3 | ||||
|
2
| ||
| 3 |
即二面角S-BC-A的正切值为
2
| ||
| 3 |
点评:本题是中档题,考查空间几何体的直线与直线的位置关系,几何体的体积的求法,空间的二面角的平面角,考查空间想象能力、逻辑推理能力、计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
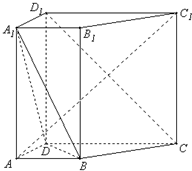 如图,在直四棱柱ANCD-A1B1C1D1中,已知DC=DD1=2AD=2AB=2,AD⊥DC,AB∥DC.
如图,在直四棱柱ANCD-A1B1C1D1中,已知DC=DD1=2AD=2AB=2,AD⊥DC,AB∥DC.