题目内容
5. 在△ABC中,D为BC中点,AD=3.
在△ABC中,D为BC中点,AD=3.(1)当BC=4,AB=4时,求AC的长;
(2)当∠BAC=90°时,求△ABC周长的最大值;
(3)当∠BAD=45°,∠CAD=30°时,求△ABC的面积.
分析 (1)利用cos∠ADB=-cos∠ADC,建立方程,求AC的长;
(2)当∠BAC=90°时,周长l=6+6cosB+6sinB,利用三角函数知识求△ABC周长的最大值;
(3)当∠BAD=45°,∠CAD=30°时,求出AB,AC,即可求△ABC的面积.
解答 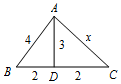 解:(1)设AC=x,
解:(1)设AC=x,
∵cos∠ADB=-cos∠ADC,
∴$\frac{{{3^2}+4-{4^2}}}{2×2×3}=-\frac{{{3^2}+{2^2}-{x^2}}}{2×2×3}$,
∴$x=\sqrt{10}$;
(2)∠BAC=90°时,则BC=2AD=6
∴周长l=6+6cosB+6sinB,
$l=6+6\sqrt{2}sin({B+\frac{π}{4}})≤6+6\sqrt{2}$
∴最大值$6+6\sqrt{2}$当且仅当$B=\frac{π}{4}$成立
(3)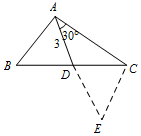
延长AD至E,使得AD=DE,∴ABEC为平行四边形
∴$\frac{AC}{sin45°}=\frac{6}{sin105°}=\frac{EC}{sin30°}$,
∴$AC=3\sqrt{2}(\sqrt{6}-\sqrt{2})$,$EC=AB=3(\sqrt{6}-\sqrt{2})=AB$,
∴S=$\frac{1}{2}AB•AC•sin75°$=9($\sqrt{3}$-1).
点评 本题考查余弦定理、正弦定理的运用,考查三角函数知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
15.已知数列{an}的首项为7,且${a_n}=\frac{1}{2}{a_{n-1}}+3({n≥2})$,则a6=( )
| A. | $\frac{193}{32}$ | B. | $\frac{385}{64}$ | C. | $\frac{161}{32}$ | D. | $\frac{97}{16}$ |
16.设函数f(x)=$\left\{\begin{array}{l}{-x+λ,x<1}\\{{2}^{x},x≥1}\end{array}\right.$(λ∈R),若对任意的a∈R都有f(f(a))=2f(a)成立,则λ的取值范围是( )
| A. | (0,2] | B. | [0,2] | C. | (-∞,2) | D. | [2,+∞) |
13.设变量x,y满足线性约束条件$\left\{\begin{array}{l}x-y+5≥0\\ x+y≥0\\ x≤3\end{array}\right.$则目标函数z=2x+4y的最小值是( )
| A. | 6 | B. | -2 | C. | 4 | D. | -6 |
10.已知函数f(x)=2sinxcosx-sin2x+1,当x=θ时函数y=f(x)取得最小值,则$\frac{sin2θ+cos2θ}{sin2θ-cos2θ}$=( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |