题目内容
10.已知函数f(x)=2sinxcosx-sin2x+1,当x=θ时函数y=f(x)取得最小值,则$\frac{sin2θ+cos2θ}{sin2θ-cos2θ}$=( )| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
分析 将函数f(x)=2sinxcosx-sin2x+1化解求解最小值,求出θ,带入$\frac{sin2θ+cos2θ}{sin2θ-cos2θ}$化解计算即可.
解答 解:函数f(x)=2sinxcosx-sin2x+1=sin2x+$\frac{1}{2}$cos2x+$\frac{1}{2}$=$\frac{\sqrt{5}}{2}$sin(2x+φ)+$\frac{1}{2}$,
其中tanφ=$\frac{1}{2}$,可得cotφ=2.
当x=θ时函数y=f(x)取得最小值,即2θ+φ=$-\frac{π}{2}+2kπ$,
那么:2θ=$-\frac{π}{2}-$φ+2kπ.
则$\frac{sin2θ+cos2θ}{sin2θ-cos2θ}$=$\frac{tan2θ+1}{tan2θ-1}$=$\frac{tan(-\frac{π}{2}-φ)+1}{tan(-\frac{π}{2}-φ)-1}$=$\frac{-tan(\frac{π}{2}+φ)+1}{-tan(\frac{π}{2}+φ)-1}$=$\frac{-cotφ+1}{-cotφ-1}=3$
故选B.
点评 本题主要考察了三角函数的诱导公式和辅助角公式,“弦化切”的思想.属于中档题.

练习册系列答案
相关题目
20.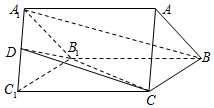 如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.
(Ⅰ)求证:A1B∥平面B1CD;
(Ⅱ)当三棱锥C-B1C1D体积最大时,求点B到平面B1CD的距离.
 如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.(Ⅰ)求证:A1B∥平面B1CD;
(Ⅱ)当三棱锥C-B1C1D体积最大时,求点B到平面B1CD的距离.
18.已知函数$f(x)=\left\{\begin{array}{l}{e^x}+m\;-1,x≥0\\ ax+b,x<0\end{array}\right.$其中m<-1,对于任意x1∈R且x1≠0,均存在唯一实数x2,使得f(x2)=f(x1),且x1≠x2,若|f(x)|=f(m)有4个不相等的实数根,则a的取值范围是( )
| A. | (0,1) | B. | (-1,0) | C. | (-2,-1)∪(-1,0) | D. | (-2,-1) |
5. 在△ABC中,D为BC中点,AD=3.
在△ABC中,D为BC中点,AD=3.
(1)当BC=4,AB=4时,求AC的长;
(2)当∠BAC=90°时,求△ABC周长的最大值;
(3)当∠BAD=45°,∠CAD=30°时,求△ABC的面积.
 在△ABC中,D为BC中点,AD=3.
在△ABC中,D为BC中点,AD=3.(1)当BC=4,AB=4时,求AC的长;
(2)当∠BAC=90°时,求△ABC周长的最大值;
(3)当∠BAD=45°,∠CAD=30°时,求△ABC的面积.
15.在平面直角坐标系中,角α的终边经过点(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则sinα的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
19.平面内的动点(x,y)满足约束条件$\left\{\begin{array}{l}{x+y-3≤0}\\{x-y+1≤0}\end{array}\right.$,则z=2x+y的取值范围是( )
| A. | (-∞,+∞) | B. | (-∞,4] | C. | [4,+∞) | D. | [-2,2] |