题目内容
15.设函数f(x)=2x-a,g(x)=x+2.(1)当a=1时,求不等式f(x)+f(-x)≤g(x)的解集;
(2)求证:$f({\frac{b}{2}}),f({-\frac{b}{2}}),f({\frac{1}{2}})$中至少有一个不小于$\frac{1}{2}$.
分析 (1)利用绝对值的意义,分类讨论,即可求不等式f(x)+f(-x)≤g(x)的解集;
(2)利用反证法证明即可.
解答 (1)解:当a=1时,|2x-1|+|2x+1|≤x+2,
$\left\{{\begin{array}{l}{x≤-\frac{1}{2}}\\{-4x≤x+2}\end{array}}\right.$无解;$\left\{{\begin{array}{l}{-\frac{1}{2}<x<\frac{1}{2}}\\{2≤x+2}\end{array}}\right.$,解得$0≤x<\frac{1}{2}$;$\left\{{\begin{array}{l}{x≥\frac{1}{2}}\\{4x≤x+2}\end{array}}\right.$,解得$\frac{1}{2}≤x≤\frac{2}{3}$.
综上,不等式的解集为$\left\{{x|0≤x≤\frac{2}{3}}\right\}$.
(2)证明:若$f({\frac{b}{2}}),f({-\frac{b}{2}}),f({\frac{1}{2}})$都小于$\frac{1}{2}$,
则$\left\{{\begin{array}{l}{-\frac{1}{2}<a+b<\frac{1}{2}}\\{-\frac{1}{2}<a-b<\frac{1}{2}}\\{-\frac{1}{2}<1-a<\frac{1}{2}}\end{array}}\right.$,前两式相加得$-\frac{1}{2}<a<\frac{1}{2}$与第三式$\frac{1}{2}<a<\frac{3}{2}$矛盾.故$f({\frac{b}{2}}),f({-\frac{b}{2}}),f({\frac{1}{2}})$中至少有一个不小于$\frac{1}{2}$.
点评 本题考查绝对值不等式的解法,考查反证法的运用,考查学生分析解决问题的能力,属于中档题.

 金钥匙试卷系列答案
金钥匙试卷系列答案 在△ABC中,D为BC中点,AD=3.
在△ABC中,D为BC中点,AD=3.(1)当BC=4,AB=4时,求AC的长;
(2)当∠BAC=90°时,求△ABC周长的最大值;
(3)当∠BAD=45°,∠CAD=30°时,求△ABC的面积.
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 5$\sqrt{2}$ | D. | $\sqrt{10}$ |
| A. | y2=8x | B. | y2=-8x | C. | x2=8y | D. | x2=-8y |
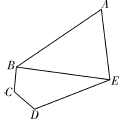 某学校的平面示意图为如下图五边形区域ABCDE,其中三角形区域ABE为生活区,四边形区域BCDE为教学区,AB,BC,CD,DE,EA,BE为学校的主要道路(不考虑宽度).$∠BCD=∠CDE=\frac{2π}{3}$,$∠BAE=\frac{π}{3},DE=3BC=3CD=\frac{9}{10}km$.
某学校的平面示意图为如下图五边形区域ABCDE,其中三角形区域ABE为生活区,四边形区域BCDE为教学区,AB,BC,CD,DE,EA,BE为学校的主要道路(不考虑宽度).$∠BCD=∠CDE=\frac{2π}{3}$,$∠BAE=\frac{π}{3},DE=3BC=3CD=\frac{9}{10}km$. 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点.