题目内容
15.已知数列{an}的首项为7,且${a_n}=\frac{1}{2}{a_{n-1}}+3({n≥2})$,则a6=( )| A. | $\frac{193}{32}$ | B. | $\frac{385}{64}$ | C. | $\frac{161}{32}$ | D. | $\frac{97}{16}$ |
分析 由已知数列递推式可得数列{an-6}是以1为首项,以$\frac{1}{2}$为公比的等比数列,求出等比数列的通项公式,可得an,则a6可求.
解答 解:由${a_n}=\frac{1}{2}{a_{n-1}}+3({n≥2})$,得${a}_{n}-6=\frac{1}{2}({a}_{n-1}-6)$(n≥2),
∵a1-6=7-6=1≠0,
∴$\frac{{a}_{n}-6}{{a}_{n-1}-6}=\frac{1}{2}$,即数列{an-6}是以1为首项,以$\frac{1}{2}$为公比的等比数列,
∴${a}_{n}-6=1×(\frac{1}{2})^{n-1}$,即${a}_{n}=(\frac{1}{2})^{n-1}+6$,
则${a}_{6}=(\frac{1}{2})^{5}+6=\frac{193}{32}$.
故选:A.
点评 本题考查数列递推式,考查了由数列递推式构造等比数列求数列的通项公式,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

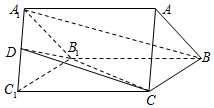 如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点. 在△ABC中,D为BC中点,AD=3.
在△ABC中,D为BC中点,AD=3.