题目内容
7.定积分$\int_1^e{(2x+\frac{1}{x})}dx$的值为( )| A. | e2-1 | B. | e2 | C. | e2+1 | D. | e2+2 |
分析 根据积分公式直接进行计算即可.
解答 解:$\int_1^e{(2x+\frac{1}{x})}dx$=(x2+lnx)|${\;}_{1}^{e}$=e2+lne-12-ln1=e2,
故选:B.
点评 本题主要考查积分的计算,要求熟练掌握常见函数的积分公式,比较基础.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
15.设函数f(2x+1)=${3}^{4{x}^{2}+2x}$,则f(1)=( )
| A. | 0 | B. | 1 | C. | 3 | D. | 36 |
18.已知角θ的始边与x轴的非负半轴重合,终边在直线y=$\frac{1}{2}$x上,则cos2θ=( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
12.已知$\overrightarrow{a}$=5$\overrightarrow{e}$,$\overrightarrow{b}$=-3$\overrightarrow{e}$,$\overrightarrow{c}$=4$\overrightarrow{e}$,则2$\overrightarrow{a}$-3$\overrightarrow{b}$+$\overrightarrow{c}$=( )
| A. | 5$\overrightarrow{e}$ | B. | -5$\overrightarrow{e}$ | C. | 23$\overrightarrow{e}$ | D. | -23$\overrightarrow{e}$ |
19.已知A(3,1),B(-1,2),则直线AB的斜率为( )
| A. | $\frac{1}{7}$ | B. | 0 | C. | $-\frac{1}{4}$ | D. | -3 |
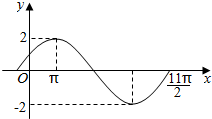 已知函数$f(x)=Asin(ωx+\frac{π}{6})(A>0,ω>0)$)图象的一部分如图所示.
已知函数$f(x)=Asin(ωx+\frac{π}{6})(A>0,ω>0)$)图象的一部分如图所示.