题目内容
等比数列{an}的前n项和Sn,且a3=
,S3=
,求an的表达式.
| 3 |
| 2 |
| 9 |
| 2 |
考点:等比数列
专题:计算题,等差数列与等比数列
分析:讨论q=1和q≠1的情况,分别应用等比数列的通项公式和求和公式,解方程即可得到公比和首项,进而得到通项公式.
解答:
解:当q=1时,a3=a1=
,S3=3a1=
,an=
;
当q≠1时,由S3=
=
且a3=a1q2=
,
得a1=6,q=-
,an=6•(-
)n-1.
综上可得:an=
或者an=6•(-
)n-1.
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
当q≠1时,由S3=
| a1(1-q3) |
| 1-q |
| 9 |
| 2 |
| 3 |
| 2 |
得a1=6,q=-
| 1 |
| 2 |
| 1 |
| 2 |
综上可得:an=
| 3 |
| 2 |
| 1 |
| 2 |
点评:本题考查等比数列的通项和求和,注意公比为1的情况,考查运算能力,属于基础题和易错题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
复数
(i为虚数单位)的虚部是( )
| -i |
| 2i-1 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
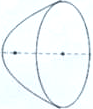 汽车前灯反射镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反射镜的轴垂直,灯泡位于抛物线的焦点出,已知灯口直径是26厘米,灯深11厘米,那灯泡与反射镜的顶点距离为
汽车前灯反射镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反射镜的轴垂直,灯泡位于抛物线的焦点出,已知灯口直径是26厘米,灯深11厘米,那灯泡与反射镜的顶点距离为