题目内容
已知函数f(x)=sinx,x∈[-
,
],若f(sinα)+f(cosα-
)=0,则sinα•cosα= .
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
考点:二倍角的正弦
专题:三角函数的求值
分析:利用函数f(x)的奇偶性和单调性即可得到结论.
解答:
解:函数f(x)=sinx,x∈[-
,
],则函数f(x)是奇函数且函数单调递增,
若f(sinα)+f(cosα-
)=0,
则f(cosα-
)=-f(sinα)=f(-sinα),
则cosα-
=-sinα,
即sinα+cosα=
,
平方得1+2sinα•cosα=
,
解得sinα•cosα=-
,
故答案为:-
| π |
| 2 |
| π |
| 2 |
若f(sinα)+f(cosα-
| 1 |
| 2 |
则f(cosα-
| 1 |
| 2 |
则cosα-
| 1 |
| 2 |
即sinα+cosα=
| 1 |
| 2 |
平方得1+2sinα•cosα=
| 1 |
| 4 |
解得sinα•cosα=-
| 3 |
| 8 |
故答案为:-
| 3 |
| 8 |
点评:本题主要考查三角函数求值,利用同角的三角函数的关系式是解决本题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知集合A={x|x=2n,n∈N*},B={x|x=2n,n∈N*},则下列不正确的是( )
| A、A⊆B |
| B、A∩B=A |
| C、B∩(∁zA)=Φ |
| D、A∪B=B |
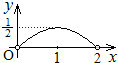
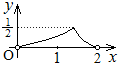
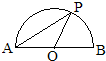 如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x函数关系的图象大致是( )
如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x函数关系的图象大致是( )