题目内容
6.设集合A={x|x<3},B={x|2x>4},则A∩B=( )| A. | ∅ | B. | {x|0<x<3} | C. | {x|1<x<3} | D. | {x|2<x<3} |
分析 求解指数不等式化简集合B,然后直接利用交集运算求解
解答 解:∵B={x|2x>4}={x|x>2},
又A={x|x<3},
∴A∩B={x|2<x<3},
故选:D
点评 本题考查了交集及其运算,考查了一元二次不等式及指数不等式的解法,是基础的计算题.

练习册系列答案
相关题目
1.函数y=loga(x+3)-1(a>0且a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中m>0,n>0,则$\frac{1}{m}+\frac{1}{n}$的最小值为( )
| A. | $3+2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | 4+2$\sqrt{3}$ | D. | $4\sqrt{3}$ |
9.已知函数y=f(x2-2x)在区间(-∞,-1]上单调递增,在区间[1,3]上是减函数,则y=f(x)( )
| A. | 在区间(-∞,3]上递增 | B. | 在区间(-∞,-1]上递增 | ||
| C. | 在区间(-∞,3]上递减 | D. | 在区间(-∞,-1]上递减 |
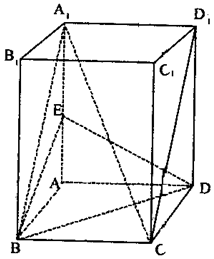 如图,在长方体ABCD-A1B1C1D1中,棱AD=DC=3,DD1=4,E是A1A的中点.
如图,在长方体ABCD-A1B1C1D1中,棱AD=DC=3,DD1=4,E是A1A的中点.