题目内容
15.根据下列条件,解三角形.(Ⅰ)已知 b=4,c=8,B=30°,求C,A,a;
(Ⅱ)在△ABC中,B=45°,C=75°,b=2,求a,c,A.
分析 (Ⅰ)由条件利用正弦定理求得sinC的值,可得C为直角,求得A,再由勾股定理求得a的值.
(Ⅱ)由条件利用三角形内角和公式求得A的值,再利用正弦定理求得a的值.
解答 解:(Ⅰ)已知△ABC中,∵已知b=4,c=8,B=30°,
由正弦定理可$\frac{b}{sinB}=\frac{c}{sinC}$,得sinC=1,可得C=90°,A=60°
∴a=$\sqrt{{c}^{2}-{b}^{2}}=4\sqrt{3}$,
(Ⅱ)∵已知△ABC中,B=45°,C=75°,b=2,由三角形内角和公式可得A=60°,
由正弦定理可得$\frac{a}{sinA}=\frac{b}{sinB}$=$\frac{c}{sinC}$,得a=$\sqrt{6}$,c=$\sqrt{3}+1$
点评 本题主要考查了三角形内角和公式、正弦定理的应用,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
5.已知α是第四象限角,sin($\frac{5π}{2}$+α)=$\frac{1}{5}$,那么tan α等于( )
| A. | -$\frac{2\sqrt{6}}{5}$ | B. | -2$\sqrt{6}$ | C. | 2$\sqrt{6}$ | D. | $\frac{2\sqrt{6}}{5}$ |
6.设集合A={x|x<3},B={x|2x>4},则A∩B=( )
| A. | ∅ | B. | {x|0<x<3} | C. | {x|1<x<3} | D. | {x|2<x<3} |
3.若方程$\frac{{x}^{2}}{10-k}$+$\frac{{y}^{2}}{5-k}$=1表示双曲线,则k的取值范围是( )
| A. | (5,10) | B. | (-∞,5) | C. | (10,+∞) | D. | (-∞,5)∪(10,+∞) |
10.设集合 M={x||x|≤2,x∈R},N={x|x2≤4,x∈N},则( )
| A. | M=N | B. | M?N | C. | M?N | D. | M∩N=∅ |
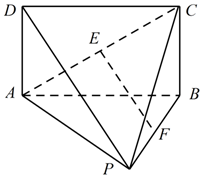 如图,在几何体P-ABCD中,平面ABCD⊥平面PAB,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点.
如图,在几何体P-ABCD中,平面ABCD⊥平面PAB,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点.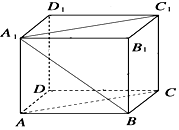 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求直线A1B与平面ACC1A1所成角的正弦值.
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求直线A1B与平面ACC1A1所成角的正弦值.