题目内容
17.已知动圆过定点P(2,0),且在y轴上截得弦长为4.(1)求动圆圆心的轨迹Q的方程;
(2)已知点E(m,0)为一个定点,过E点分别作斜率为k1、k2的两条直线l1、l2,直线l1交轨迹Q于A、B两点,直线l2交轨迹Q于C、D两点,线段AB、CD的中点分别是M、N.若k1+k2=1,求证:直线MN恒过定点,并求出该定点的坐标.
分析 (1)设动圆圆心为O1(x,y),动圆与y轴交于R,S两点,由题意,得|O1P|=|O1S|,由此得到$\sqrt{{x^2}+{2^2}}$=$\sqrt{{{(x-2)}^2}+{y^2}}$,从而能求出动圆圆心的轨迹Q的方程.
(2)由$\left\{\begin{array}{l}y={k_1}(x-m)\\{y^2}=4x\end{array}\right.$,得${k_1}{y^2}-4y-4{k_1}m=0$,由已知条件推导出M、N的坐标,由此能证明直线MN恒过定点(m,2).
解答 解:(1)设动圆圆心为O1(x,y),动圆与y轴交于R,S两点.
由题意,得|O1P|=|O1S|.
当O1不在y轴上时,过O1作O1H⊥RS交RS于H,则H是RS的中点.
∴|O1S|=$\sqrt{{x^2}+{2^2}}$.
又|O1P|=$\sqrt{{{(x-2)}^2}+{y^2}}$,
∴$\sqrt{{x^2}+{2^2}}$=$\sqrt{{{(x-2)}^2}+{y^2}}$,化简得y2=4x(x≠0).
又当O1在y轴上时,O1与O重合,点O1的坐标为(0,0)也满足方程y2=4x.
∴动圆圆心的轨迹Q的方程为y2=4x.
(2)证明:由$\left\{\begin{array}{l}y={k_1}(x-m)\\{y^2}=4x\end{array}\right.$,得${k_1}{y^2}-4y-4{k_1}m=0$.
设A(x1,y1),B(x2,y2),则${y_1}+{y_2}=\frac{4}{k_1},\;{y_1}{y_2}=-4m$.
因为AB中点$M(\frac{{{x_1}+{x_2}}}{2},\frac{{{y_1}+{y_2}}}{2})$,所以$M(\frac{2}{k_1^2}+m,\frac{2}{k_1})$.
同理,点$N(\frac{2}{k_2^2}+m,\frac{2}{k_2})$.
∴${k_{MN}}=\frac{{{y_M}-{y_N}}}{{{x_M}-{x_N}}}=\frac{{{k_1}{k_2}}}{{{k_1}+{k_2}}}={k_1}{k_2}$
∴直线MN:$y-\frac{2}{k_1}={k_1}{k_2}[x-(\frac{2}{k_1^2}+m)]$,即y=k1k2(x-m)+2
∴直线MN恒过定点(m,2).
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、斜率计算公式,考查了推理能力与计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案①5,9,100,107,111,121,180,195,200,265,
②7,34,61,88,115,142,169,196,223,250;
③30,57,84,111,138,165,192,219,246,270;
④11,38,65,92,119,146,173,200,227,254;
关于上述样本的下列结论中,正确的是( )
| A. | ②、④都可能为分层抽样 | B. | ①、③都不能为分层抽样 | ||
| C. | ①、④都可能为系统抽样 | D. | ②、③都不能为系统抽样 |
| A. | -$\frac{2\sqrt{6}}{5}$ | B. | -2$\sqrt{6}$ | C. | 2$\sqrt{6}$ | D. | $\frac{2\sqrt{6}}{5}$ |
| A. | ∅ | B. | {x|0<x<3} | C. | {x|1<x<3} | D. | {x|2<x<3} |
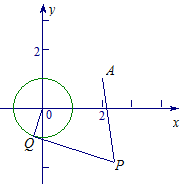 已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|.
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|.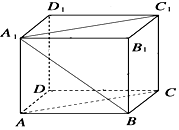 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求直线A1B与平面ACC1A1所成角的正弦值.
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求直线A1B与平面ACC1A1所成角的正弦值.