题目内容
18.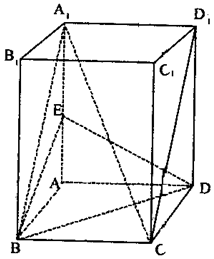 如图,在长方体ABCD-A1B1C1D1中,棱AD=DC=3,DD1=4,E是A1A的中点.
如图,在长方体ABCD-A1B1C1D1中,棱AD=DC=3,DD1=4,E是A1A的中点.(1)求证:A1C∥平面BED;
(2)求二面角E-BD-A的正切值.
分析 (1)建立空间直角坐标系,先求得相关点的坐标,从而得到$\overrightarrow{{A}_{1}C}$=(3,3,-4),$\overrightarrow{EO}$=($\frac{3}{2}$,$\frac{3}{2}$,-2),然后由共线向量定理证明即可.
(2)分别求得二个半平面的一个法向量即可,由于AE⊥平面ABCD,则$\overrightarrow{AE}$=(0,0,2)就是平面ABCD的法向量.B(3,0,0),D(0,3,0),再求得平面EBD的一个法向量为,用向量的夹角公式求解.
解答 (1)证明:如图建立空间直角坐标系,取BD的中点O,连接EO.
A1(0,0,4),C(3,3,0),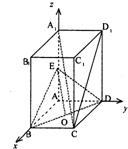 E(0,0,2),O($\frac{3}{2}$,$\frac{3}{2}$,0)(2分)
E(0,0,2),O($\frac{3}{2}$,$\frac{3}{2}$,0)(2分)
$\overrightarrow{{A}_{1}C}$=(3,3,-4),$\overrightarrow{EO}$=($\frac{3}{2}$,$\frac{3}{2}$,-2),
∴$\overrightarrow{{A}_{1}C}$=2$\overrightarrow{EO}$,∴A1C∥EO.
∵EO?平面BED,A1C?平面BED,
∴A1C∥平面BED.(5分)
(2)解:由于AE⊥平面ABCD,
则$\overrightarrow{AE}$=(0,0,2)就是平面ABCD的法向量.(6分)
B(3,0,0),D(0,3,0),
$\overrightarrow{BE}$=(-3,0,2),$\overrightarrow{BD}$=(-3,3,0),
设平面EBD的法向量为$\overrightarrow{n}$=(x,y,z).
得$\left\{\begin{array}{l}{-3x+2z=0}\\{-3x+3y=0}\end{array}\right.$
令z=3,则$\overrightarrow{n}$=(2,2,3).(7分)
cos$<\overrightarrow{n},\overrightarrow{AE}>$=$\frac{6}{2\sqrt{17}}$,
∴二面角E-BD-A的正切值为$\frac{2\sqrt{2}}{3}$.(10分)
点评 本题主要考查用空间坐标法来求二面角,线面平行,作为向量法在解决立体几何中的平行,垂直,角和距离有不可比拟的优越性,要灵活运用.

 阅读快车系列答案
阅读快车系列答案| A. | ∅ | B. | {x|0<x<3} | C. | {x|1<x<3} | D. | {x|2<x<3} |
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | b<c<a |
| A. | (5,10) | B. | (-∞,5) | C. | (10,+∞) | D. | (-∞,5)∪(10,+∞) |
| A. | M=N | B. | M?N | C. | M?N | D. | M∩N=∅ |
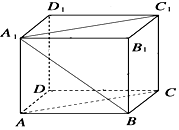 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求直线A1B与平面ACC1A1所成角的正弦值.
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求直线A1B与平面ACC1A1所成角的正弦值.