题目内容
设数列{bn}的前n项和为Tn，已知bn=
，求证：Tn＜
．
| 1 |
| 22n-1 |
| 7 |
| 8 |
考点：数列的求和
专题：等差数列与等比数列
分析：由已知条件得到Tn=
+
+
+
+
+…+
＜
+
+
+
+
+…+
，由此能证明Tn＜
．
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 24 |
| 1 |
| 28 |
| 1 |
| 216 |
| 1 |
| 22n-1 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 24 |
| 1 |
| 26 |
| 1 |
| 28 |
| 1 |
| 22(n-1) |
| 7 |
| 8 |
解答：
解：∵bn=
，
∴Tn=
+
+
+
+
+…+
＜
+
+
+
+
+…+
=
+
=
+
(1-
)
＜
+
=
＜
．
∴Tn＜
．
| 1 |
| 22n-1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 24 |
| 1 |
| 28 |
| 1 |
| 216 |
| 1 |
| 22n-1 |
＜
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 24 |
| 1 |
| 26 |
| 1 |
| 28 |
| 1 |
| 22(n-1) |
=
| 1 |
| 2 |
| ||||
1-
|
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4n-1 |
＜
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 6 |
| 7 |
| 8 |
∴Tn＜
| 7 |
| 8 |
点评：本题考查不等式的证明，是中档题，解题时要认真审题，注意放缩法的合理运用．
练习册系列答案
相关题目
已知α，β表示两个不同的平面，m为平面α内的一条直线，则“α⊥β”是“m⊥β”的（ ）
| A、充要条件 |
| B、充分不必要 |
| C、既不充分也不必要 |
| D、必要不充分 |
设集合M={-1，0，1}，N={0，1}，则M∩N等于（ ）
| A、{-1，0，1} | B、{0，1} |
| C、{1} | D、{0} |
已知复数z=
，
是z的共轭复数，则z•
=（ ）
| ||
1-
|
. |
| z |
. |
| z |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
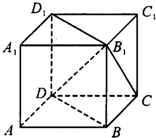如图，在正方体ABCD-A1B1C1D1中，