题目内容
函数f(x)=x+
-m在(0,3]上有且仅有一个零点,则实数m的取值范围是 .
| 2 |
| x |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:首先,设双钩函数g(x)=x+
,然后,求解该函数的值域,再结合零点的概念,利用双钩函数g(x)与直线y=m的交点情形,从而得到实数m的取值范围.
| 2 |
| x |
解答:
解:函数f(x)=x+
-m的零点,也就是方程x+
-m=0的根,
设函数g(x)=x+
,
∴g ′ (x)=1-
,
∵g′(x)=0,
∴x=
,
当0<x<
时,g′(x)>0,函数的减区间为(0,
),
g(x)∈(2
,+∞),
当
≤x≤3时,g′(x)<0,函数的增区间为[
,3],
g(x)∈[2
,
],
函数的零点就是g(x)=m的解,
∴m>
或m=2
,函数f(x)=x+
-m在(0,3]上有且仅有一个零点,
故答案为{m|m>
或m=2
}.
| 2 |
| x |
| 2 |
| x |
设函数g(x)=x+
| 2 |
| x |
∴g ′ (x)=1-
| 2 |
| x2 |
∵g′(x)=0,
∴x=
| 2 |
当0<x<
| 2 |
| 2 |
g(x)∈(2
| 2 |
当
| 2 |
| 2 |
g(x)∈[2
| 2 |
| 11 |
| 3 |
函数的零点就是g(x)=m的解,
∴m>
| 11 |
| 3 |
| 2 |
| 2 |
| x |
故答案为{m|m>
| 11 |
| 3 |
| 2 |
点评:本题重点考查函数的零点,注意将问题等价转化,可以求解函数的值域问题.

练习册系列答案
相关题目
设an是(1-
)n的展开式中x项的系数(n=2,3,4,…),若bn=
,则bn的最大值是( )
| x |
| an+1 | ||
(n+7)
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

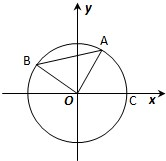 如图,A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴的交点,△AOB为正三角形.若A点的坐标为(x,y).记∠COA=α,求|BC|2的取值范围.
如图,A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴的交点,△AOB为正三角形.若A点的坐标为(x,y).记∠COA=α,求|BC|2的取值范围.