��Ŀ����
12����֪������ϵ�ļ�����ƽ��ֱ������ϵ��ԭ��O����������x����������غϣ��ҳ��ȵ�λ��ͬ������C�ķ�����$��=2\sqrt{2}sin����-\frac{��}{4}��$��ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}x=2+tcos��\\ y=1+tsin��\end{array}\right.$��tΪ������0�ܦ����У�����P��2��1����ֱ��l������C����A��B���㣮��1������=0ʱ����|AB|�ij��ȣ�
��2����|PA|2+|PB|2��ȡֵ��Χ��
���� ��1���Ѽ����귽�̻�Ϊֱ�����귽�̣��������ɵó���
��2����t1��t2Ϊ��Ӧ����ֵt2+6tcos��+7=0������0��cos2����$\frac{7}{9}$�����ø���ϵ���Ĺ�ϵ�ɵ�|PA|2+|PB|2=��-6cos����2-14���ɵó���
��� �⣺��1������C�ķ�����$��=2\sqrt{2}sin����-\frac{��}{4}��$����Ϊ��2=2��sin��-2��cos�ȣ�
��x2+y2=2y-2x��
����C�ķ���Ϊ��x+1��2+��y-1��2=2��
����=0ʱ��ֱ��l��y=1��
��������C�ɵ�x+1=��2�����x=1��-3��
��|AB|=4��
��2����t1��t2Ϊ��Ӧ����ֵt2+6tcos��+7=0������0����cos2����$\frac{7}{9}$
��t1+t2=-6cos����t1t2=7��
��|PA|2+|PB|2=��-6cos����2-14��
��|PA|2+|PB|2�ʣ�14��22]��
���� ���⿼���˰Ѽ����귽�̻�Ϊֱ�����귽�̡�һԪ���η��̵ĸ���ϵ���Ĺ�ϵ�������ļ������壬������������������������������е��⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
20���ڡ�ABC�У���A��B��C���Եı߷ֱ�Ϊa��b��c������c=3��$a=3\sqrt{2}$��$cosB=\frac{{\sqrt{2}}}{4}$����sinA=��������
| A�� | $\frac{7}{24}$ | B�� | $\frac{{3\sqrt{7}}}{8}$ | C�� | $\frac{{\sqrt{2}}}{4}$ | D�� | $\frac{{\sqrt{14}}}{4}$ |
1��ԲM�ķ��̣�x2+y2+2x-2y-2=0������Բ��M�����꼰�뾶rΪ��������
| A�� | M��-1��1����r=2 | B�� | M��-1��1����r=4 | C�� | M��1��-1����r=2 | D�� | M��1��-1����r=4 |
2������x�IJ���ʽ|x2-3x|��kx-x2-9��x��[1��5]�Ϻ��������ʵ��k��ȡֵ��ΧΪ��������
| A�� | ��-�ޣ�6] | B�� | ��-�ޣ�6�� | C�� | ��0��6] | D�� | [6��+�ޣ� |
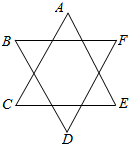 ��4�ֲ�ͬ����ɫ��ͼ��A��B��C��D��E��F���������Ⱦɫ��Ҫ��ͬһ�߶ε����㣨�磺AC��BD��������ɫ����ͬ���������ڵ����㣨�磺AB��BC��������ɫҲ����ͬ����ͬ��Ⱦɫ��������Ϊ96 ������ѧ���𣩣�
��4�ֲ�ͬ����ɫ��ͼ��A��B��C��D��E��F���������Ⱦɫ��Ҫ��ͬһ�߶ε����㣨�磺AC��BD��������ɫ����ͬ���������ڵ����㣨�磺AB��BC��������ɫҲ����ͬ����ͬ��Ⱦɫ��������Ϊ96 ������ѧ���𣩣�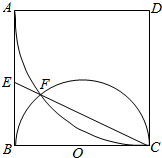 ��ͼ���ı���Ϊ�߳�Ϊa�������Σ���DΪԲ�ģ�DAΪ�뾶��Բ������BCΪֱ����ԲO����C��F������CF���ӳ���AB�ڵ�E��
��ͼ���ı���Ϊ�߳�Ϊa�������Σ���DΪԲ�ģ�DAΪ�뾶��Բ������BCΪֱ����ԲO����C��F������CF���ӳ���AB�ڵ�E��