题目内容

求证：
sin(
π
2
+θ)-cos(π-θ)
sin(
π
2
-θ)-sin(π-θ)
=
2
1-tanθ
．
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：所证等式左边利用诱导公式化简，再分子分母除以cosθ，利用同角三角函数间基本关系弦化切后，得到结果与右边相等，得证．
解答： 解：左边=
cosθ+cosθ
cosθ-sinθ
=
2cosθ
cosθ-sinθ
=
2
1-tanθ
=右边，
则原式成立．
点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．
练习册系列答案
相关题目
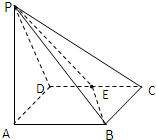如图，四棱锥P-ABCD中，ABCD为菱形，PA⊥平面ABCD，∠BCD=60°，BC=1，E为CD的中点，PC与平面ABCD成角60°
（1）求证：平面EPB⊥平面PBA；
（2）求二面角B-PD-A的平面角正切值的大小．
已知
a
=（cosα，sinα），
b
=（cosβ，sinβ），
a
•
b
=
1
3
，cosα=
1
7
，0＜β＜α＜
π
2
，求sinβ的值．
设函数f（x）的定义域为[-1，1]，求函数y=f（
x
2
）+f（
1
x
）的定义域．
设两集合A、B，求证：当且仅当A⊆B时，A∩B=A成立．
已知函数y=3-4cos（2x+
π
3
），x∈[-
π
6
，
π
6
]，求该函数的最大值、最小值及相应的x值．
已知方程（3m+7）x2+（3m+4）y2=5m+12表示的曲线是椭圆，求实数m的取值．
设
π
6
是函数f（x）=sin（2x+θ）的一个零点，则函数在区间（0，2π）内所有极值点之和为
 
．
设实数a，b，c满足a2+b2≤c≤1，则a+b+c的最小值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网