题目内容
15.已知a,b,c分别为△ABC的三个内角A,B,C的对边,c=2,且sin2A+sin2B=sinAsinB+sin2C,则△ABC面积的最大值为( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
分析 利用正余弦定理化简,求出C角的大小,利用基本不等式求解即可.
解答 解:∵sin2A+sin2B=sinAsinB+sin2C,
由正弦定理可得:a2+b2=ab+c2,
则cosC=$\frac{a^2+b^2-{c}^{2}}{2ab}$=$\frac{1}{2}$,
∴C=$\frac{π}{3}$.
∵c=2,
∴a2+b2=ab+4,
可得ab+4≥2ab,解得ab≤4.(当且仅当a=b时取等号)
那么:△ABC面积$S=\frac{1}{2}absinC$$≤\frac{1}{2}×4×sin\frac{π}{3}=\sqrt{3}$.
故选C.
点评 本题考查了正余弦定理化简计算能力和基本不等式的运用求最值问题.属于基础题.

练习册系列答案
相关题目
6.下列四个函数中,既是奇函数又在定义域上单调递减的是( )
| A. | y=2-|x| | B. | y=tanx | C. | y=-x3 | D. | $y={log_{\frac{1}{5}}}x$ |
3.下列说法正确的是( )
| A. | 若x,y∈R,且$\left\{\begin{array}{l}{x+y>4}\\{xy>4}\end{array}\right.$,则$\left\{\begin{array}{l}{x>2}\\{y>2}\end{array}\right.$ | |
| B. | 设命题p:?x>0,x2>2x,则¬p:?x0≤0,x02≤2${\;}^{{x}_{0}}$ | |
| C. | △ABC中,A>B是sinA>sinB的充分必要条件 | |
| D. | 命题“若a=-1,则f(x)=ax2+2x-1只有一个零点”的逆命题为真 |
10.设全集U=R,集合A={x|x2-1<0},B={x|x(x-3)>0}则A∩(∁UB)=( )
| A. | {x|0<x<2} | B. | {x|0<x<1} | C. | {x|0≤x<1} | D. | {x|-1<x<0} |
20.已知点F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,点B是短轴顶点,直线BF2与椭圆C相交于另一点D.若△F1BD是等腰三角形,则椭圆C的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
4.已知$\overrightarrow{a}$,$\overrightarrow{b}$是两个向量,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,且($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,若在△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,D为BC中点,则AD的长为( )
| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
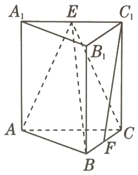 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.