��Ŀ����
3������˵����ȷ���ǣ�������| A�� | ��x��y��R����$\left\{\begin{array}{l}{x+y��4}\\{xy��4}\end{array}\right.$����$\left\{\begin{array}{l}{x��2}\\{y��2}\end{array}\right.$ | |
| B�� | ������p��?x��0��x2��2x����Vp��?x0��0��x02��2${\;}^{{x}_{0}}$ | |
| C�� | ��ABC�У�A��B��sinA��sinB�ij�ֱ�Ҫ���� | |
| D�� | ���⡰��a=-1����f��x��=ax2+2x-1ֻ��һ����㡱��������Ϊ�� |
���� A����x��y��R����$\left\{\begin{array}{l}{x+y��4}\\{xy��4}\end{array}\right.$����$\left\{\begin{array}{l}{x��2}\\{y��2}\end{array}\right.$�Ǽ����⣬����x=1��y=5��
B��������p��?x��0��x2��2x����Vp��?x0��0��x02��2��
C����ABC��A��B?2RsinA��2RsinB?a��b��
D��f��x��=ax2+2x-1ֻ��һ����㣬⇒a=0��a=-1��
��� �⣺����A����x��y��R����$\left\{\begin{array}{l}{x+y��4}\\{xy��4}\end{array}\right.$����$\left\{\begin{array}{l}{x��2}\\{y��2}\end{array}\right.$�Ǽ����⣬����x=1��y=5���ʴ���
����B��������p��?x��0��x2��2x����Vp��?x0��0��x02��2���ʴ���
����C����ABC�У�A��B?2RsinA��2RsinB?a��b������ȷ��
����D��f��x��=ax2+2x-1ֻ��һ����㣬⇒a=0��a=-1���ʴ���
��ѡ��C
���� ���⿼���˺�������������ٵ��ж��������������ʽ����Ҫ�������ж��������е��⣮

��ϰ��ϵ�д�
 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
�����Ŀ
13����g��x��=2x-1��f[g��x��]=$\frac{1+{x}^{2}}{3{x}^{2}}$����f��-3��=��������
| A�� | 1 | B�� | $\frac{2}{3}$ | C�� | $\sqrt{3}$ | D�� | $\frac{{\sqrt{3}}}{3}$ |
11������{an}��ǰn���Sn=n2-5n��n��N*������p-q=4����ap-aq=��������
| A�� | 20 | B�� | 16 | C�� | 12 | D�� | 8 |
18������˵����ȷ���ǣ�������
| A�� | ����x=$\frac{��}{4}$����tanx=1���������������� | |
| B�� | �ڡ�ABC�У�sinA��sinB�ij�Ҫ������A��B | |
| C�� | ����f��x��=sinx+$\frac{4}{sinx}$��x�ʣ�0���У�����СֵΪ4 | |
| D�� | ?x��R��ʹ��sinx•cosx=$\frac{3}{5}$ |
15����֪a��b��c�ֱ�Ϊ��ABC�������ڽ�A��B��C�ĶԱߣ�c=2����sin2A+sin2B=sinAsinB+sin2C�����ABC��������ֵΪ��������
| A�� | 1 | B�� | 2 | C�� | $\sqrt{3}$ | D�� | $2\sqrt{3}$ |
12����ֱ֪��a��b�Լ�ƽ������£�������������ȷ���ǣ�������
| A�� | ��a�Φ���b�Φ�����a��b | B�� | ��a�Φ���b�ͦ����� a��b | ||
| C�� | ��a��b��b�Φ�����a�Φ� | D�� | ��a�ͦ���b�Φ£��� ���ͦ� |
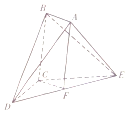 ����ͼ��ʾ�Ķ�����ABCDE�У��ı���ABCFΪƽ���ı��Σ�FΪDE���е㣬��BCEΪ����ֱ�������Σ�BEΪб�ߣ���BDEΪ�������Σ�CD=CE=2��
����ͼ��ʾ�Ķ�����ABCDE�У��ı���ABCFΪƽ���ı��Σ�FΪDE���е㣬��BCEΪ����ֱ�������Σ�BEΪб�ߣ���BDEΪ�������Σ�CD=CE=2��