题目内容
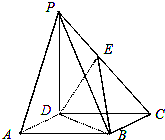 如图所示,在底面是正方形的四棱锥PABCD中,PD⊥底面ABCD,PD=DC,E是PC的中点.
如图所示,在底面是正方形的四棱锥PABCD中,PD⊥底面ABCD,PD=DC,E是PC的中点.(1)证明:PA∥平面BDE;
(2)求二面角B-DE-C的余弦值.
考点:用空间向量求平面间的夹角,直线与平面平行的判定
专题:空间位置关系与距离,空间向量及应用
分析:(1)画出图形,结合图形,连接AC,交BD于O,连OE,易证OE∥PA,即证PA∥平面BDE;
(2)以D为坐标原点,DA、DC、DP所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,
求出平面DEC的法向量
,平面DBE的法向量
,利用法向量求出二面角B-DE-C的余弦值.
(2)以D为坐标原点,DA、DC、DP所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,
求出平面DEC的法向量
| DA |
| n |
解答:
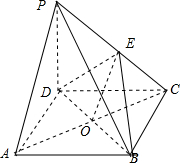 解:(1)证明:如图所示,连接AC,交BD于O,连OE,
解:(1)证明:如图所示,连接AC,交BD于O,连OE,
∵E是PC的中点,O是AC的中点,
∴OE∥PA;
又∵OE?平面BDE,PA?平面BDE,
∴PA∥平面BDE;
(2)以D为坐标原点,DA、DC、DP所在的直线分别为x轴、y轴、z轴,建立空间直角坐标系,
令PD=DC=1,则平面DEC的法向量是
=(1,0,0),
设平面DBE的法向量为
=(x,y,z),
∵
⊥
,
⊥
,
且
=(1,1,0),
=(0,
,
);
∴
,
得
=(1,-1,1);
cos<
,
>=
=
=
,
由题意知二面角B-DE-C的平面角为锐角,
∴二面角B-DE-C的余弦值为
.
 解:(1)证明:如图所示,连接AC,交BD于O,连OE,
解:(1)证明:如图所示,连接AC,交BD于O,连OE,∵E是PC的中点,O是AC的中点,
∴OE∥PA;
又∵OE?平面BDE,PA?平面BDE,
∴PA∥平面BDE;
(2)以D为坐标原点,DA、DC、DP所在的直线分别为x轴、y轴、z轴,建立空间直角坐标系,
令PD=DC=1,则平面DEC的法向量是
| DA |
设平面DBE的法向量为
| n |
∵
| n |
| DB |
| n |
| DE |
且
| DB |
| DE |
| 1 |
| 2 |
| 1 |
| 2 |
∴
|
得
| n |
cos<
| DA |
| n |
| ||||
|
|
| 1×1-1×0+1×0 | ||
1×
|
| ||
| 3 |
由题意知二面角B-DE-C的平面角为锐角,
∴二面角B-DE-C的余弦值为
| ||
| 3 |
点评:本题考查了空间中的平行与垂直的应用问题,也考查了空间直角坐标系以及空间向量的应用问题,是中档题目.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
下列两集合表示同一集合的是( )
| A、M={1,2},N={(1,2)} |
| B、M={y=lgx2},N={y=2lgx} |
| C、M={x|x+y=1},N={y|x+y=1} |
| D、M={y|y=x2},N={y|y=2x} |
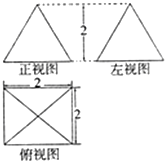
某几何体的三视图如图所示,根据图中标出的数据,可得这个几何体的体积为( )

A、4+4
| ||
B、4+4
| ||
C、
| ||
| D、12 |
下列说法中:
①所有幂函数的图象都经过点(1,1)和(0,0);
②所有幂函数的图象都不经过第四象限;
③函数y=x0的图象是一条直线;
④幂函数可能是奇函数,也可能是偶函数,也可能既不是奇函数也不是偶函数;
正确说法的个数是( )
①所有幂函数的图象都经过点(1,1)和(0,0);
②所有幂函数的图象都不经过第四象限;
③函数y=x0的图象是一条直线;
④幂函数可能是奇函数,也可能是偶函数,也可能既不是奇函数也不是偶函数;
正确说法的个数是( )
| A、0 | B、1 | C、2 | D、3 |
有一抛物线型拱桥,当水面离拱顶2米时,水面宽4米,则当水面下降1米后,水面宽度为( )
| A、9 | ||
| B、4.5 | ||
C、
| ||
D、2
|