题目内容
化简:sin(2nπ+
)•cos(nπ+
)(n∈Z).
| 2π |
| 3 |
| 4π |
| 3 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:首先,根据诱导公式,得到原式=
×cos(nπ+
),然后,对n的取值情况进行分类讨论即可.
| ||
| 2 |
| 4π |
| 3 |
解答:
解:原式=sin
cos(nπ+
)
=
×cos(nπ+
)
当n=2k,k∈Z时,
原式=
×(-
)=-
,
当n=2k+1,k∈Z时,
原式=
×
=
,
| 2π |
| 3 |
| 4π |
| 3 |
=
| ||
| 2 |
| 4π |
| 3 |
当n=2k,k∈Z时,
原式=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
当n=2k+1,k∈Z时,
原式=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
点评:本题重点考查了三角函数诱导公式及其灵活应用,常见角的三角函数等知识,属于中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
“直线a2x-y+6=0与直线4x-(a-3)y+9=0互相垂直”是“a=-1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
集合P={(x,y)|(x-2cosθ)2+(y-2sinθ)2=1,0≤θ≤2π},集合Q={(x,y)|y≥
x},若P⊆Q,则θ的取值范围是( )
| ||
| 3 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
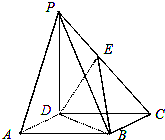 如图所示,在底面是正方形的四棱锥PABCD中,PD⊥底面ABCD,PD=DC,E是PC的中点.
如图所示,在底面是正方形的四棱锥PABCD中,PD⊥底面ABCD,PD=DC,E是PC的中点.