题目内容
已知函数f(x)=
,若f(a)=f(b)=f(c)(其中a<b<c),则abc的取值范围是 .
|
考点:分段函数的应用
专题:函数的性质及应用
分析:作出函数f(x)的图象,根据图象确定a,b,c的取值范围,即可求出abc的取值范围.
解答:
 解:∵a,b,c互不相等,
解:∵a,b,c互不相等,
∴不妨设a<b<c,
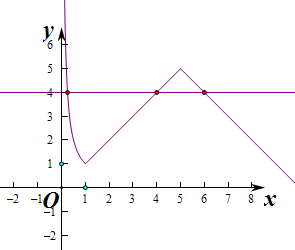
作出函数f(x)的图象如图:
则由图象可知0<a<1,1<b<5,
则由f(a)=f(b),得e|lna|=e|lnb|,
即-lna=lnb,
即lna+lnb=lnab=0,
∴ab=1,
即abc=c,
由10-x=1,
解得x=9,
∴5<c<9,
∴abc=c∈(5,9),
故答案为:(5,9)
 解:∵a,b,c互不相等,
解:∵a,b,c互不相等,∴不妨设a<b<c,
作出函数f(x)的图象如图:
则由图象可知0<a<1,1<b<5,
则由f(a)=f(b),得e|lna|=e|lnb|,
即-lna=lnb,
即lna+lnb=lnab=0,
∴ab=1,
即abc=c,
由10-x=1,
解得x=9,
∴5<c<9,
∴abc=c∈(5,9),
故答案为:(5,9)
点评:本题主要考查函数的交点的应用,利用对数函数的运算性质得到ab=1是解决本题的关键,结合数形结合是解决本题的突破点.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
下列说法正确的是( )
| A、0∈N* | ||
B、
| ||
| C、0∈∅ | ||
| D、-2∈Z |
圆C1的方程为x2+y2=
,圆C2的方程(x-cosθ)2+(y-sinθ)2=
(θ∈R),过C2上任意一点P作圆C1的两条切线PM、PN,切点分别为M、N,则∠MPN的最大值为( )
| 4 |
| 25 |
| 1 |
| 25 |
A、
| ||
B、
| ||
C、
| ||
D、
|
集合P={(x,y)|(x-2cosθ)2+(y-2sinθ)2=1,0≤θ≤2π},集合Q={(x,y)|y≥
x},若P⊆Q,则θ的取值范围是( )
| ||
| 3 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
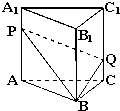 如图,已知直三棱柱ABC-A1B1C1,点P、Q分别在棱AA1和CC1上,AP=C1Q,则平面BPQ把三棱柱分成两部分的体积比为( )
如图,已知直三棱柱ABC-A1B1C1,点P、Q分别在棱AA1和CC1上,AP=C1Q,则平面BPQ把三棱柱分成两部分的体积比为( )| A、2:1 | B、3:1 |
| C、3:2 | D、4:3 |
设x,y满足约束条件
且,z=x+ay的最小值为17,则a=( )
|
| A、-7 | B、5 |
| C、-7或5 | D、-5或7 |
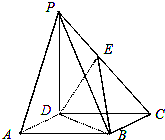 如图所示,在底面是正方形的四棱锥PABCD中,PD⊥底面ABCD,PD=DC,E是PC的中点.
如图所示,在底面是正方形的四棱锥PABCD中,PD⊥底面ABCD,PD=DC,E是PC的中点.