题目内容
3.复数$\frac{1-i}{3+4i}$(其中i是虚数单位)在复平面内对应的点所在的象限为( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数的运算法则、几何意义即可得出.
解答 解:复数$\frac{1-i}{3+4i}$=$\frac{(1-i)(3-4i)}{(3+4i)(3-4i)}$=$\frac{-1-7i}{25}$,在复平面内对应的点$(-\frac{1}{25},-\frac{7}{25})$所在的象限为第三象限.
故选:C.
点评 本题考查了复数的运算法则、几何意义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
14.一个由底面是正三角形的三棱柱和三棱锥组成的组合体,其三视图如图所示,则该组合体的体积为( )
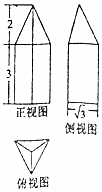

| A. | $\frac{11\sqrt{3}}{3}$ | B. | $\frac{15\sqrt{3}}{4}$ | C. | $\frac{11\sqrt{3}}{4}$ | D. | 5$\sqrt{3}$ |
18.已知平面向量$\vec a=({1,2}),\vec b=({-2,m})$,且$\vec a∥\vec b$,则$|{\vec b}|$为( )
| A. | 2$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | 1 |
8.已知函数f(x)=sin(x+φ)-$\sqrt{3}$cos(x+φ)(|φ|<$\frac{π}{2}$)的图象关于直线x=π对称,则cos2φ=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
15.定义:$|{\begin{array}{l}a&b\\ c&d\end{array}}|=ad-bc$,如$|{\begin{array}{l}1&2\\ 3&4\end{array}}|=1×4-2×3=-2$,则$|{\begin{array}{l}{\int_1^2{xdx}}&3\\ 1&2\end{array}}|$=( )
| A. | 0 | B. | $\frac{3}{2}$ | C. | 3 | D. | 6 |
7.已知复数zi=($\frac{i+1}{i-1}$)2016(i为虚数单位),则z=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
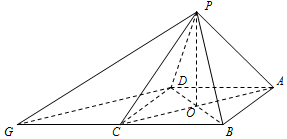 在四棱锥P-ABCD中,底面ABCD为菱形,∠PAD=∠PAB,AC交BD于O,
在四棱锥P-ABCD中,底面ABCD为菱形,∠PAD=∠PAB,AC交BD于O,