题目内容
向量
=(an+1-
,
),
=(3,3)且
∥
,a1=5,则数列{an}的前10项和为( )
| v |
| an |
| 2 |
| an+12 |
| 2an |
| μ |
| v |
| μ |
| A、50 | B、100 |
| C、150 | D、200 |
考点:数列的求和,平面向量共线(平行)的坐标表示
专题:等差数列与等比数列
分析:由已知条件推导出(an+1-an)2=0,由a1=5,得an=5,由此能求出数列{an}的前10项和.
解答:
解:∵向量
=(an+1-
,
),
=(3,3)且
∥
,
∴
=
,
整理,得(an+1-an)2=0,
∵a1=5,∴an=5,
∴数列{an}的前10项和为:10×5=50.
故选:A.
| v |
| an |
| 2 |
| an+12 |
| 2an |
| μ |
| v |
| μ |
∴
an+1-
| ||
| 3 |
| ||
| 3 |
整理,得(an+1-an)2=0,
∵a1=5,∴an=5,
∴数列{an}的前10项和为:10×5=50.
故选:A.
点评:本题考查数列的前10项和的求法,是基础题,解题时注意向量平行的条件的合理运用.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
已知函数f(x)=
,若f(a-1)+f(a)>0,则实数a的取值范围是( )
|
A、a>
| ||
| B、a>1 | ||
C、a<
| ||
| D、a<1 |
函数f(x)=
•
的定义域是( )
| 4-x |
| x+1 |
| A、[-1,+∞) |
| B、(-∞,-1] |
| C、[-1,4] |
| D、(-1,4) |
下列命题中是真命题的是( )
| A、若函数lgf(x)为奇函数,则函数f(x)为奇函数 |
| B、若函数lgf(x)为偶函数,则函数f(x)为偶函数 |
| C、若函数sinf(x)为奇函数,则函数f(x)为奇函数 |
| D、若函数sinf(x)为偶函数,则函数f(x)为偶函数 |
已知点A、B、C为椭圆
+y2=1上三点,其中A(1,
),且△ABC的内切圆圆心在直线x=1上,则△ABC三边斜率和为( )
| x2 |
| 4 |
| ||
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
某种产品的广告费支出x与销售额y(单位:万元)之间有下表关系
y与x的线性回归方程为
=6.5x+a,当广告支出是3万元时,则销售额大约为( )
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
 |
| y |
| A、36 | B、37 | C、39 | D、40 |
设底面为等边三角形的直棱柱的体积为V,则其表面积最小时,底面边长为( )
A、
| |||
B、
| |||
C、
| |||
D、
|
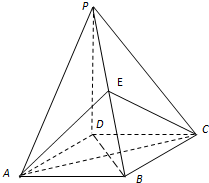 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.