题目内容
已知函数f（x）=
，若f（a-1）+f（a）＞0，则实数a的取值范围是（ ）
|
A、a＞
| ||
| B、a＞1 | ||
C、a＜
| ||
| D、a＜1 |
考点：函数单调性的性质
专题：计算题,函数的性质及应用
分析：由函数f（x）=
，可得函数在R上单调递减，且为奇函数，利用f（a-1）+f（a）＞0，可求实数a的取值范围．
|
解答：
解：∵函数f（x）=
，
∴函数在R上单调递减，且为奇函数，
∵f（a-1）+f（a）＞0，
∴f（a-1）＞f（-a），
∴a-1＜-a，
∴a＜
．
故选：C．
|
∴函数在R上单调递减，且为奇函数，
∵f（a-1）+f（a）＞0，
∴f（a-1）＞f（-a），
∴a-1＜-a，
∴a＜
| 1 |
| 2 |
故选：C．
点评：本题考查了函数奇偶性和单调性的综合应用，比较基础．
练习册系列答案
相关题目
问题：
①某社区有500个家庭，其中高收入家庭125户，中等收入家庭280户，低收入家庭95户，为了了解社会购买力的某项指标，要从中抽出一个容量为100户的样本；
②从10名学生中抽出3人参加座谈会．
方法：Ⅰ简单随机抽样法；Ⅱ系统抽样法；Ⅲ分层抽样法；此题中所提问题与抽样方法配对正确的是（ ）
①某社区有500个家庭，其中高收入家庭125户，中等收入家庭280户，低收入家庭95户，为了了解社会购买力的某项指标，要从中抽出一个容量为100户的样本；
②从10名学生中抽出3人参加座谈会．
方法：Ⅰ简单随机抽样法；Ⅱ系统抽样法；Ⅲ分层抽样法；此题中所提问题与抽样方法配对正确的是（ ）
| A、①Ⅲ；②Ⅰ |
| B、①Ⅰ；②Ⅱ |
| C、①Ⅱ；②Ⅲ |
| D、①Ⅲ；②Ⅱ |
数列{an}（n∈Z）中，“an+1+an=an+1+an+2”是数列{an}是等差数列的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
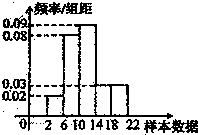若容量为100的某样本的频率分布直方图如图所示，则根据该频率分布直方图可以估计出样本数据落在[14，18）内的频数a的值为（ ）| A、8 | B、12 | C、32 | D、36 |
设a＞b，则：①ac2＞bc2，②2a＞2b，③
＜
，④a3＞b3，⑤|a|＞|b|，其中正确的结论有（ ）
| 1 |
| a |
| 1 |
| b |
| A、1个 | B、2个 |
| C、3 个 | D、4个 |
向量
=（an+1-
，
），
=（3，3）且
∥
，a1=5，则数列{an}的前10项和为（ ）
| v |
| an |
| 2 |
| an+12 |
| 2an |
| μ |
| v |
| μ |
| A、50 | B、100 |
| C、150 | D、200 |
已知
，
是两个夹角为
的单位向量，
=3
-2
，
=k
+
，若
⊥
，则实数k的值为（ ）
| e1 |
| e2 |
| π |
| 3 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、1 |